数组操作
1. 基本操作
1.1 创建数组
| 操作 | 示例 | 说明 |
|---|---|---|
np.zeros() | np.zeros(10, dtype=int) | 创建一个长度为 10 的数组,数组的值都是 0 |
np.ones() | np.ones((3,5), dtype=float) | 创建一个 3×5 的浮点型数组,数组的值都是 1 |
np.full() | np.full((3,5), 3.14) | 创建一个 3×5 的浮点型数组,数组的值都是 3.14 |
np.arange(start, stop, step) | np.arange(0, 20, 2) | 创建一个整型数组,数组的值是一个线性序列(左闭右开) |
np.linspace(start, stop, num) | np.linspace(0, 1, 5) | 创建一个 5 个元素的数组,这 5 个数均匀地分配到 0~1(闭区间) |
np.asarray(array_like) | >>> a = [1, 2] >>> np.asarray(a) array([1, 2]) | 把一个 array_like 的对象转换为 ndarray。输入类型可为 lists, lists of tuples, tuples, tuples of tuples, tuples of lists, ndarray |
np.random.random() | np.random.random((3, 3)) | 创建一个 3×3 的、在 0~1 均匀分布的随机数组成的数组 |
np.random.rand() | ||
np.random.uniform() | uniform(low=0.0, high=1.0, size=None) | 创建一个在[low, high)之间均匀分布的大小为 size 的随机数组, size 为 int or tuple of ints |
np.random.normal() | np.random.normal(0, 1, (3,3)) | 创建一个 3×3 的、均值为 0、方差为 1 的 正态分布的随机数数组 |
np.random.randint() | np.random.randint(0, 10, (3,3)) | 创建一个 3×3 的、[0, 10)区间的随机整型数组 |
np.eye() | np.eye(3) | 创建一个 3*3 的单位矩阵 |
np.empty() | np.empty(3) | 创建一个由 3 个 float 数组成的未初始化的数组,数组的值是内存空间中的任意值 |
np.empty_like() | np.empty_like(demo) | 创建一个形状和 demo 数组一样的未初始化的数组,默认为 int 类型 |
1.2 数组的拼接和分裂
np.concatenate():将数组元组或列表作为第一个参数,可设置axis=任意轴# 沿着第二个轴拼接(从0开始索引) np.concatenate([grid, grid], axis=1)np.vstack():垂直栈,垂直拼接,以元组或列表为参数np.hstack():水平栈,水平拼接,以元组或列表为参数np.dstack():沿第三个维度拼接,以元组或列表为参数np.split():以数组名和索引列表为参数,索引列表记录分裂点的位置,可选择axis>>> x = [1, 2, 3, 99, 99, 3, 2, 1] >>> x1, x2, x3 = np.split(x, [3, 5]) >>> print(x1, x2, x3) [1 2 3] [99 99] [3 2 1]np.hsplit():以数组名和索引列表为参数水平分裂,索引列表记录分裂点的位置np.vsplit():以数组名和索引列表为参数垂直分裂,索引列表记录分裂点的位置np.dsplit():以数组名和索引列表为参数沿第三个维度分裂,索引列表记录分裂点的位置np.transpose():生成一个数组的转置,原数组不变
1.3 数组变形
最灵活的实现方式是通过
.reshape()方法来实现:>>> grid = np.arange(1, 10).reshape((3, 3)) >>> print(grid) [[1 2 3] [4 5 6] [7 8 9]]涉及到“增维”操作时,可以在一个切片操作中利用
newaxis关键字: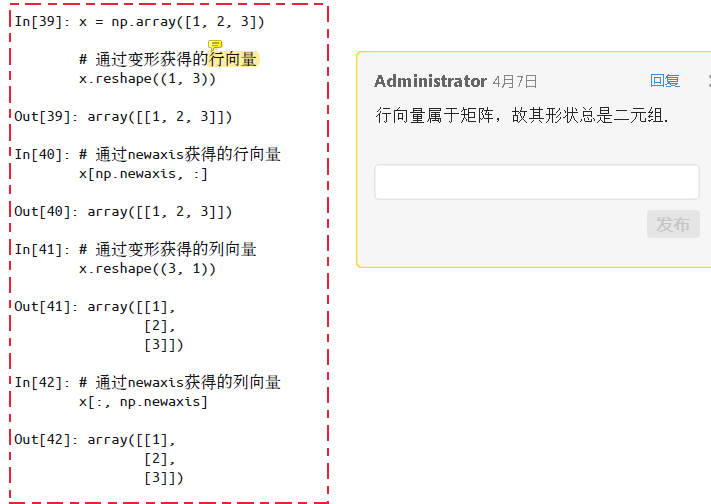
向量、行向量、列向量即使表示相同内容,但其shape(分别为(n,)、(n, 1)、(1, n) )也互不相等,这也是三个互不相同的对象。其中向量表示只带一个方括号,而行、列向量属于二维数组,总是带二个方括号。
若
M[1:4, 2:3] = array([[1.], [0.], [-1.0]]),则进行如下修改会报错:# Error M[1:4, 2:3] = array([1., 0., -1.0])
1.4 一般性方法/函数
数组的一般性方法:
.T:转置(返回视图).reshape():重塑(返回视图).copy():复制(返回副本)
数组的一般性函数:
np.allclose(a, b):判等函数——两个浮点数组的相等不是直接进行的,因为两个浮点数可能无限接近但不相等,用allclose()可指定精度相等。np.minimum(a, b):np.moveaxis(a, source, destination):维度移动(返回视图)——将数组a的某个轴source移动到新位置destination,其他轴的顺序保持不变。>>> x = np.zeros((3, 4, 5)) >>> np.moveaxis(x, 0, -1).shape (4, 5, 3) >>> np.moveaxis(x, -1, 0).shape (5, 3, 4)np.swapaxes(a, axis1, axis2):交换数组a的两个轴。>>> x = np.array([[1,2,3]]) >>> np.swapaxes(x,0,1) array([[1], [2], [3]])
1.5 数组中的交换
# 输入
a = np.array([[1, 2, 3],
[2, 3, 4],
[1, 6, 5],
[9, 3, 4]])
# 交换两行(第2、3行)为:
a[[1,2], :] = a[[2,1], :]
# 输出
a = np.array([[1, 2, 3],
[1, 6, 5],
[2, 3, 4],
[9, 3, 4]])- 若用
temp = a[1]; a[1] = a[2]; a[2] = temp,会导致交换失败。 - 若用
temp = a[1].copy(); a[1] = a[2]; a[2] = temp,则会交换成功。 - 原因是:
temp = a[1]并非a[1]的一个copy,而是一个“别名”。
2. 数组索引
2.1 常规索引
常规索引——在多维数组中,可以用逗号分隔的索引元组来获取(或修改)元素:
>>> x2
array([[3, 5, 2, 4],
[7, 6, 8, 8],
[1, 6, 7, 7]])
>>> x2[0, 0]
32.2 切片索引
NumPy切片语法和Python列表的标准切片语法相同,即
x[start:stop:step]当步长为负时,start参数和stop参数默认被交换。
以步长为负是一种非常方便的逆序数组的方式:
>>> x[::-1] # 所有元素,逆序的 array(9, 8, 7, 6, 5, 4, 3, 2, 1, 0) >>> x[5::-2] # 从索引5开始每隔一个元素逆序 array([5, 3, 1])多维数组类似:
>>> x2 array([[12, 5, 2, 4], [7, 6, 8, 8], [1, 6, 7, 7]]) >>> x2[::-1, ::-1] # 子数组维度也可以同时被逆序 array([[7, 7, 6, 1], [8, 8, 6, 7], [4, 2, 5, 12]])
在获取行时,出于语法的考虑,可以活力空的切片:
>>> print(x2[0]) # 等价于x2[0, :]数组切片返回的是数组数据的视图,而不是数值数据的副本。
- 这一点也是NumPy 数组切片和Python 列表切片的不同之处:在Python 列表中,切片是值的副本。
- 原因:这种默认的处理方式实际上非常有用,它意味着在处理非常大的数据集时,可以获取或处理这些数据集的片段,而不用复制底层的数据缓存。
- 若要创建数组的副本,可以很简单地通过
.copy()方法实现。
视图是与较大数组共享相同数据的较小数组,这与单个对象的引用类似。
numpy中切片将返回视图,而花哨索引返回的是数据的副本。
2.3 花哨索引
花哨索引(fancy indexing)和前面那些简单的索引非常类似,但是传递的是索引数组,而不是单个标量。它意味着传递一个索引数组来一次性获得多个数组元素。
利用花哨索引,结果的形状与索引数组的形状一致,而不是与被索引数组的形状一致。
>>> x = [51, 92, 14, 71, 60, 20, 82, 86, 74, 74] >>> ind = [3, 7, 4] >>> x[ind] array([71, 86, 60]) >>> ind = np.array([[3, 7], [4, 5]]) >>> x[ind] array([[71, 86], [60, 20]])在花哨索引中,索引值的配对遵循广播规则。注意,此时对应的返回值是广播后索引数组的形状。
2.4 组合索引
组合索引:花哨索引可以和其他索引方案结合起来形成更强大的索引操作。
>>> print(x)
[[0 1 3 4]
[4 5 6 7]
[8 9 10 11]]与简单索引组合
>>> x[2, [2, 0, 1]] array([10, 8, 9])与切片索引组合
>>> x[1:, 2, 0, 1] array([[6, 4, 5], [10, 8, 9]])与掩码组合
>>> mask = np.array([1, 0, 1, 0], dtype=bool) >>> x[row[:, np.newaxis], mask] array([[0, 2], [4, 6], [8, 10]])注意,索引操作中重复的索引会导致一些出乎意料的结果产生:

3. 通用函数
Python 的默认实现(被称作 CPython)处理起某些操作时非常慢,一部分原因是该语言的动态性和解释性。


NumPy 为很多类型的操作提供了非常方便的、静态类型的、可编译程序的接口,也被称作向量操作。
NumPy 数组的计算有时非常快,有时也非常慢。NumPy 变快的关键是利用向量化操作,通常 NumPy 的通用函数(ufunc) 中实现。
NumPy 中的向量操作是通过通用函数实现的:


任何通用函数都可以用outer方法获得两个不同输入数组所有元素对的函数运算结果。
3.1 运算符重载
所有这些算术运算符都是 NumPy 内置函数的简单封装器,例如+运算符就是一个 add 函数的封装器:
| 运算符 | 对应的通用函数 | 描述 |
|---|---|---|
+ | np.add | 加法运算(即 1 + 1 = 2) |
- | np.subtract | 减法运算(即 3 - 2 = 1) |
- | np.negative | 负数运算( 即 -2) |
* | np.multiply | 乘法运算( 即 2 * 3 = 6) |
/ | np.divide | 除法运算( 即 3 / 2 = 1.5) |
// | np.floor_divide | 地板除法运算(floor division,即 3 // 2 = 1) |
** | np.power | 指数运算( 即 2 ** 3 = 8) |
% | np.mod | 模 / 余数( 即 9 % 4 = 1) |
比较运算符和其对应的通用函数(其返回值是布尔数组):
| 运算符 | 对应的通用函数 |
|---|---|
== | np.equal |
!= | np.not_equal |
< | np.less |
<= | np.less_equal |
> | np.greater |
>= | np.greater_equal |
3.2 数学运算
| 通用函数 | 说明 |
|---|---|
np.absolute() | 别名 np.abs(),对数组求绝对值 |
np.sin() | |
np.cos() | |
np.tan() | |
np.arcsin() | |
np.arccos() | |
np.arctan() | |
np.exp(x) | |
np.exp2(x) | |
np.power(3, x) | |
np.log(x) | |
np.log2(x) | |
np.log10(x) | |
np.expm1() | 同 np.exp(),当 x 的值很小时,给出的值比 np.exp 的计算更精确 |
np.log1p() | 同 np.log(),当 x 的值很小时,给出的值比 np.log 的计算更精确 |
还有一个更加专用,也更加晦涩的通用函数优异来源是子模块
scipy.special。如果你希望对你的数据进行一些更晦涩的数学计算,scipy.special可能包含了你需要的计算函数。
3.3 二元通用函数的额外特性
二元通用函数有些非常有趣的聚合功能,这些聚合可以直接在对象上计算。例如,如果我们希望用一个特定的运算reduce一个数组,那么可以调用任何通用函数的reduce方法。一个reduce方法会对给定的元素和操作重复执行,直至得到单个的结果。
请注意,在一些特殊情况中,NumPy提供了专用的函数(
np.sum, np.prod, np.cumsum, np.cumprod),它们也可以实现以上reduce的功能。

3.4 通用函数的out参数
在进行大量运算时,有时候指定一个用于存放运算结果的数组是非常有用的。不同于创建临时数组,你可以用这个特性将计算结果直接写入到你期望的存储位置。所有的通用函数都可以通过 out 参数来指定计算结果的存放位置:
通用函数的out参数

这个特性也可以被用作数组视图

3.5 广播
通用函数另外一个非常有用的特性是它能操作不同大小和形状的数组,一组这样的操作被称为广播(broadcasting)。广播也是一种向量化操作,可以简单理解为用于不同大小数组的二进制通用函数(加、减、乘等)的一组规则。
NumPy广播的规则:
- 如果两个数组的维度数不相同,那么小维度数组的形状将会在最左边补1;
- 如果两个数组的形状在任何一个维度上都不匹配,那么数组的形状会沿着维度为1的维度扩展,以匹配另一个数组的形状;
- 如果两个数组的形状在任何一个维度上都不匹配,并且没有任何一个维度等于1,那么会引发异常。
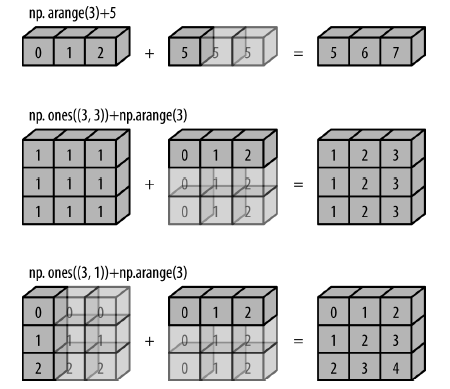
NumPy广播的可视化:
浅色的盒子表示广播的值。
需要注意的是,这个额外的内存并没有在实际操作中进行分配,但是这样的想象方式更方便我们从概念上理解。
必须恪守规则:
# M.shape = (3, 2)
# a.shape = (3,)
>>> M + a
--------------------------------------
ValueError: operands could not be broadcast together with shapes (3, 2) (3,)上例可能发生的混淆在于:你可能想通过在a数组的右边补1,而不是左边补1,让a和M的维度变得兼容。但是这不被广播的规则所允许。
如果确需右边补全,可通过数组变形来实现:
>>> a[:, np.newaxis].shape (3, 1) >>> M + a[:, np.newaxis] array([[1., 1.], [2., 2.], [3., 3.]])
假如你有一个10个观察值的数组,每个观察值包含3个数值。按照惯例,我们将用一个10×3的数组来存放该数矩:
>>> X = np.random.random((10, 3))
# 为了进一步核对我们的处理是否正确,可以查看归一化的数组的均值是否接近0:
>>> X_centered.mean(0) # 在机器精度范围内,该均值为0
array([2.22044605e-17, -7.77156117e-17, -1.66533454e-17])利用NumPy的广播和聚和功能,可以用一行代码计算矩阵的平方距离:
dist_sq = np.sum((X[:, np.newaxis, :] - X[np.newaxis, :, :]) ** 2, axis=-1)3.6 元素比较与布尔逻辑
前面已知,NumPy的通用函数可以用来代替循环,以快速实现数组的逐元素运算。同样,我们也可以用其他通用函数实现数组的逐元素比较。
如果需要统计布尔数组中True记录的个数,
可以使用np.count_nonzero()函数:
# 有多少值小于6 np.count_nonzero(x < 6)另一种方式是利用np.sum()函数:
# 有多少值小于6 np.sum(x < 6)
逐位逻辑运算符(bitwise logic operator): &, |, ^, ~ :

and和or判断整个对象是真是假,而&和|是指每个对象中的比特位。当你在NumPy中有一个布尔数组时,该数组可以被当作是由比特字符组成的:
>>> A = np.array([1, 0, 1, 0, 1, 0], dtype=bool) >>> B = np.array([1, 1, 1, 0, 1, 1], dtype=bool) >>> A | B array([True, True, True, False, True, True], dtype=bool) >>> A or B ValueError: The truth value of an array with more than one element is...
如上所述,利用比较运算符可以得到一个布尔数组,同时为了将这些值从数组中选出,可以进行简单的索引,即掩码操作——掩码操作返回的是一个一维数组,它包含了所有满足条件的值,换句话说,所有这些值是掩码数组对应位置为True的值。
>>> x < 5
array([[False, True, True, True],
[False, False, True, False],
[True, True, False, False]], dtype=bool)
>>> x [x < 5] # 为了将相应的值从数组中取出,进行掩码操作
array([0, 3, 3, 3, 2, 4])3.7 创建通用函数
将一个操作标量的函数的函数名作为参数传入vectorize()函数,将会生成一个新的“向量化”函数,新函数将遍历作用于数组中的每一个函数。
| >>> def myfunc(a, b):
| ... "Return a-b if a>b, otherwise return a+b"
| ... if a > b:
| ... return a - b
| ... else:
| ... return a + b
| >>> vfunc = np.vectorize(myfunc)
| >>> vfunc([1, 2, 3, 4], 2)
| array([3, 4, 1, 2])
| Notes
| -----
| The
vectorizefunction is provided primarily for convenience, not for| performance. The implementation is essentially a for loop.
4. 聚合
NumPy 中的一些聚合函数在 Python 中也有内置的版本,如 np.sum(), np.max(), np.min()在 Python 中内置有 sum(), max(), min()函数,但是 NumPy 的执行会更快。
默认情况下,每一个 NumPy 聚合函数返回的是整个数组的聚合结果。但是它们都可以指定 axis 参数,用于指定沿着哪个轴的方向进行聚合,即该轴将被折叠(消失)。如 axis=0, 意味着第一个轴将要被折叠——对于二维数组就是说每一列的值都将被聚合。
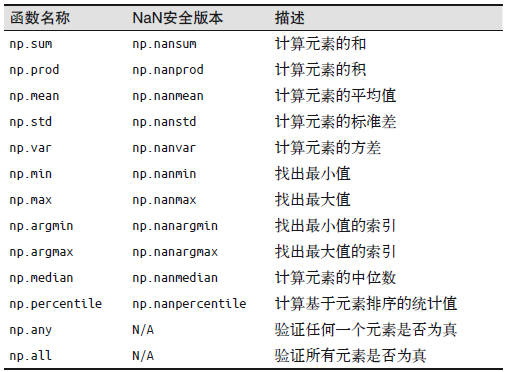
另外,大多数的聚合都有对 NaN 值的安全处理策略(NaN-safe),即计算时忽略所有的缺失值。
NumPy 中可用的聚合函数清单:
对于这些聚合函数,一种更简洁的语法形式是数组对象直接调用这些方法。
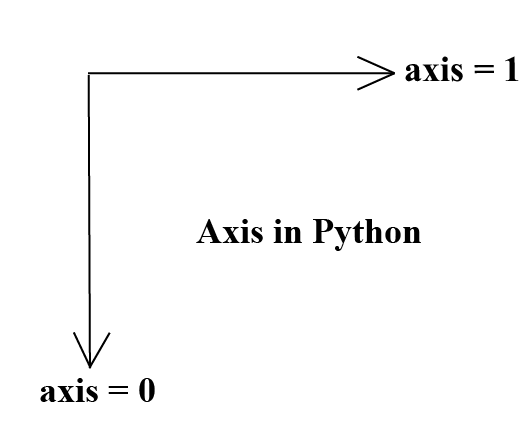
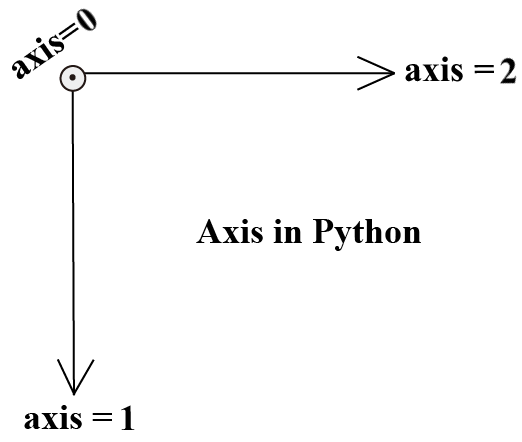
axis的方向
axis 的方向这么记:对于一个维数组,其最外侧的方括号永远表示第一维度,即,最内侧的方括号永远表示最高维度,即:
| 一维 | 二维 | 三维 |
|---|---|---|
 |  |  |
5. 数组的排序
5.1 具体方法
同样地,NumPy的np.sort函数比Python内置的sort和sorted效率更高:
>>> x = np.array([2, 1, 4, 3, 5])np.sort()函数:在不修改原数组的基础上返回一个排好序的数组>>> np.sort(x) array([1, 2, 3, 4, 5]).sort()方法:用排好序的数组替代原始数组>>> x.sort() >>> print(x) [1 2 3 4 5]np.argsort()函数:返回原始数组排好序的索引值>>> i = np.argsort(x) >>> print(i) [1 0 3 2 4]
当然,同大多数NumPy函数一样,np.sort()可设置axis参数。
5.2 排序算法
默认情况下,np.sort()的排序算法是快速排序,其复杂度为,当然也可以选择归并排序和堆排序。对于大多数情况默认的快速排序已经足够高效了。
5.3 部分排序
部分排序np.partition():
有时我们只希望找到数组中第K小的值(可为序列),
np.partition()函数提供了该功能,其输入参数为数组和数字K。输出结果是一个新数组,其中将输入数组中第K小的值放入输出数组的第K位(即其索引为K-1),往左是小于该数的所有值的任意顺序序列,往右是大于或等于该数的所有值的任意顺序序列。
>>> x = np.array([7, 2, 3, 1, 6, 5, 4]) >>> np.partition(x, 3) array([2, 1, 3, 4, 6, 5, 7])同样地,
np.argpartition()函数计算的是分隔的索引值。
K个最近邻示例

更新日志
899db-于eedbf-于47fa5-于c9215-于75141-于730b3-于0e6a3-于29df4-于c810a-于
