二叉搜索树

1. BST

二叉搜索树(binary search tree, BST)

对于一棵为 BST 的树 $T$，其三种操作的时间复杂度分别为：

操作	时间复杂度
search()	$O(height(T))$
insert()	$O(height(T))$
remove()	$O(height(T))$

2. BBST

平衡二叉搜索树(balanced binary search tree, BBST)

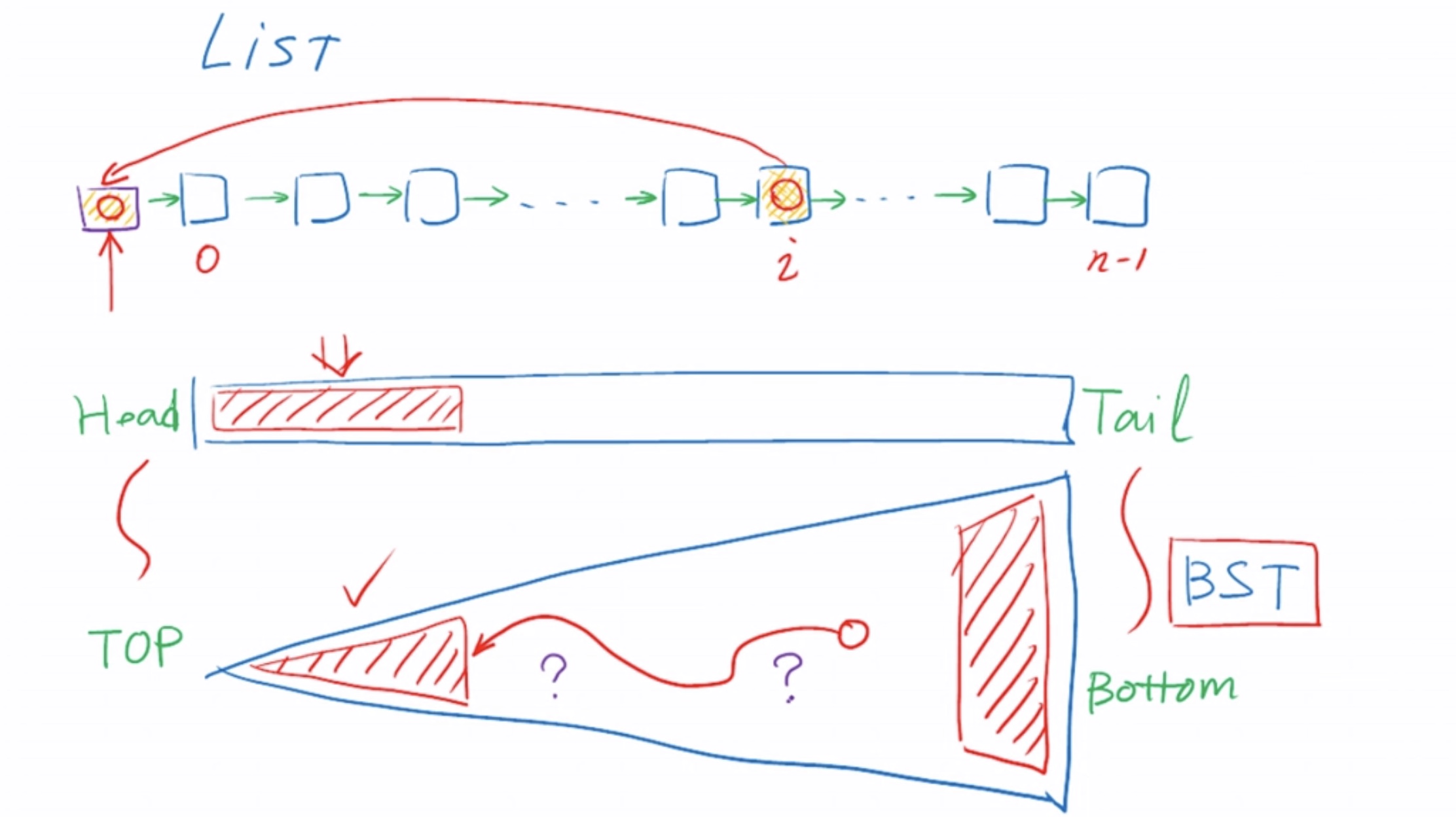
由于 BST 的search(), insert(), remove()操作均线性正比于 BST 的树高，而在最坏情况下，BST可能彻底地退化为列表，此时的查找效率甚至会降至$O(n)$，线性正比于数据集的规模。因此，若不能有效控制树高，则就实际的性能而言，较之此前的向量和列表，BST将无法体现出明显优势。

而 BBST 所做的努力，正是试图通过控制树高，使得算法效率得到提升。

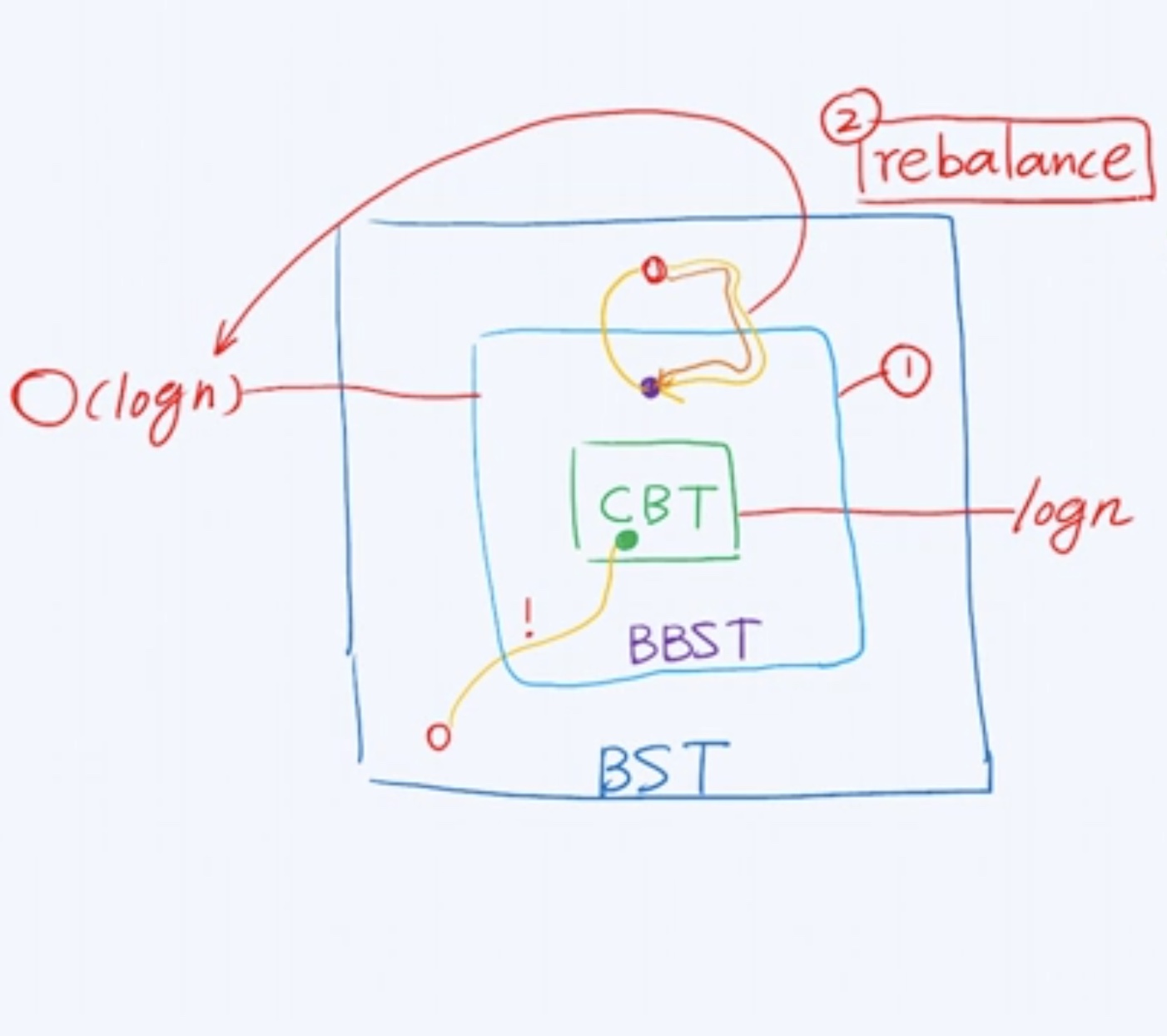
2.1 AVL树

2.2 伸展树

2.3 B-树

2.4 红黑树

2.5 kd-树