二叉树

荒流2024年2月2日大约 7 分钟约 1973 字

遍历二叉树：

遍历操作之于二叉树的意义，在于为许多相关算法的实现提供了通用框架和基本接口。
从算法策略的角度看，这一过程也等效于将半线性的树形结构转换为线性结构。

1. 算法类型

1.1 VLR, LVR, LRV 型

三种遍历方法的迭代实现均使用了辅助结构栈。与之形成对比的是，BFS型的层次遍历法使用了辅助结构队列。

三种遍历方法中：

先序遍历与后序遍历序列并非简单的逆序关系。
对于中序遍历，各节点在遍历序列中的局部次序与按照有序树定义所确定的全局左、右次序完全吻合，故而中序遍历在很多方面扮演着重要的角色。

总结而言，这三种遍历方法均可实现为非常简明的递归版，但在实际中最好使用其迭代版：

递归版与迭代版的时间复杂度在渐进意义下实际上是相同的，均为线性时间；
但递归版的时空复杂度的常系数更大，因为实现递归需要额外的程序开销。

遍历算法	示意图
先序遍历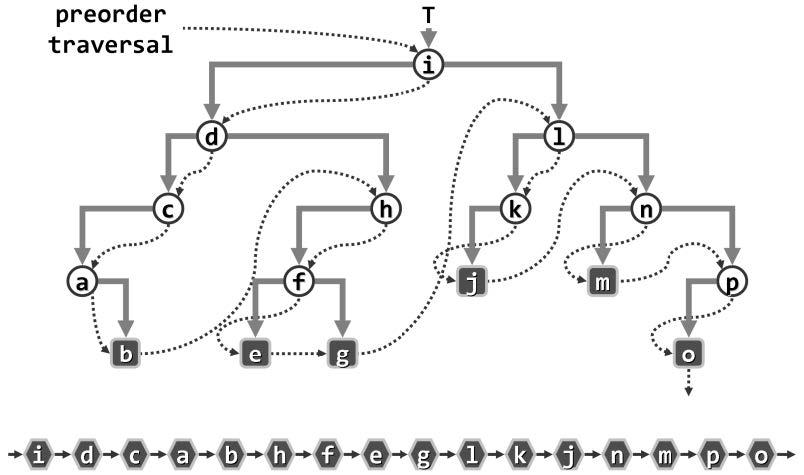
中序遍历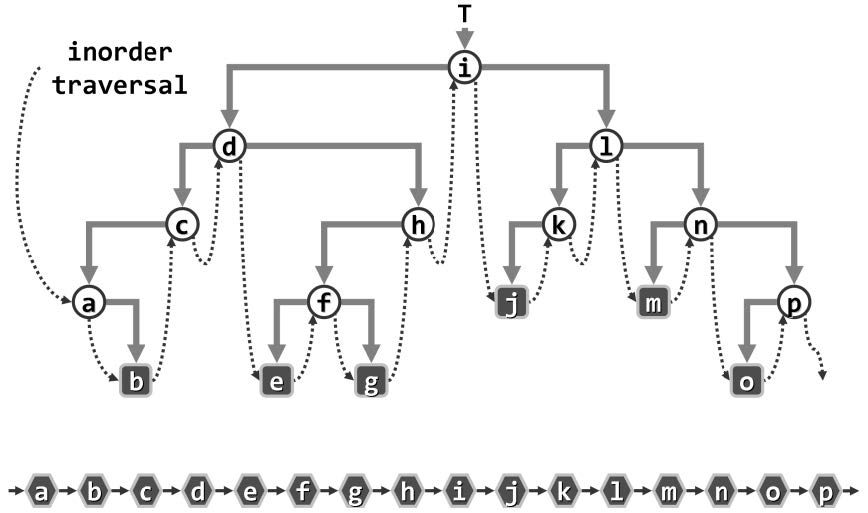
后序遍历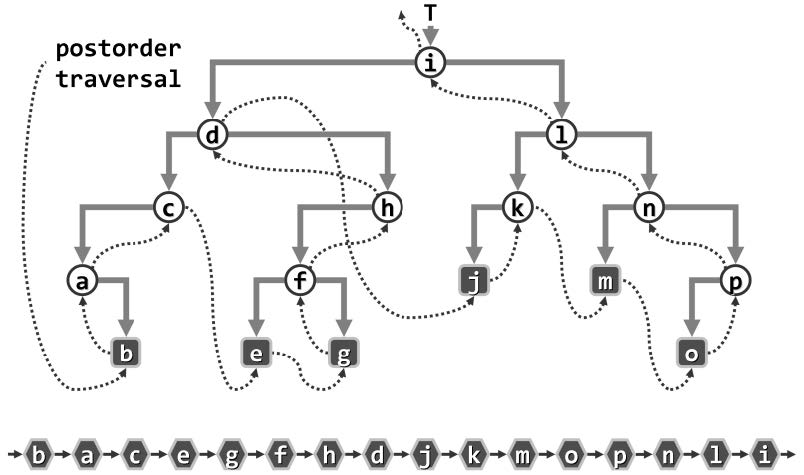

1.2 BFS 型

通常即层次遍历，其示意图如下：

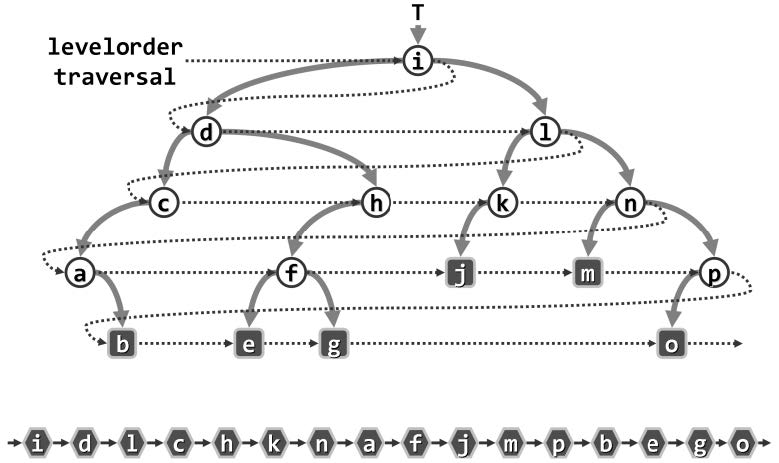
2. 先序遍历

2.1 递归式

template <typename T, typename VST> //元素类型、操作器
void travPre_R(BinNodePosi(T) x, VST& visit) { //二叉树先序遍历算法（递归版）
    if (!x) return;
    visit(x->data);
    travPre_R(x->lChild, visit);
    travPre_R(x->rChild, visit);
}

2.2 迭代式

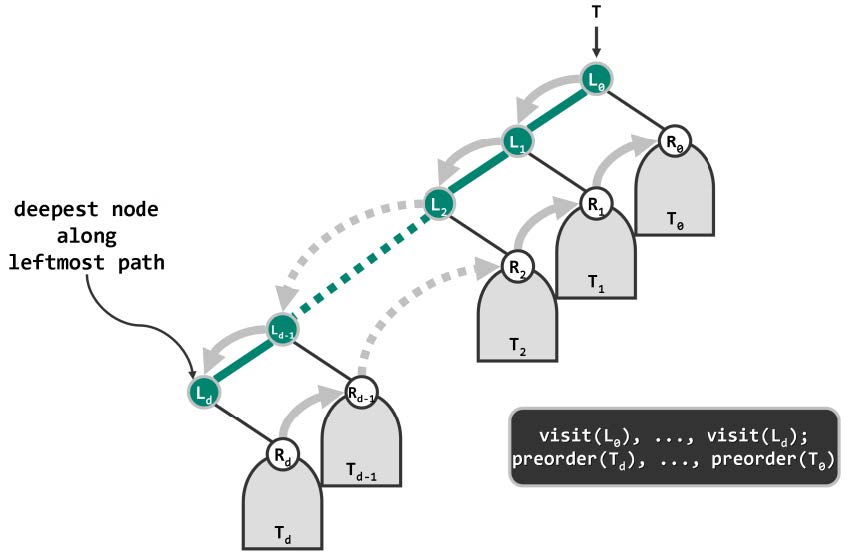
//从当前节点出发，沿左分支不断深入，直至没有左分支的节点；沿途节点遇到后立即访问
template <typename T, typename VST> //元素类型、操作器
static void visitAlongLeftBranch(BinNodePosi(T) x, VST& visit, Stack<BinNodePosi(T)>& S) {
    while (x) {
        visit(x->data); //访问当前节点
        S.push(x->rChild); //右孩子入栈暂存（可优化：通过刷断，避免空的右孩子入栈）
        x = x->lChild; //沿左分支深入一层
    }
}

template <typename T, typename VST> //元素类型、操作器
void travPre_I2(BinNodePosi(T) x, VST& visit) { //二叉树先序遍历算法（迭代版#2）
    Stack<BinNodePosi(T)> S; //辅助栈
    while (true) {
        visitAlongLeftBranch(x, visit, S); //从当前节点出发，逐批访问
        if (S.empty()) break; //直到栈空
        x = S.pop(); //弹出下一批的起点
    }
}

3. 中序遍历

3.1 递归版

template <typename T, typename VST> //元素类型、操作器
void travIn_R(BinNodePosi(T) x, VST& visit) { //二叉树中序遍历算法（递归版）
    if (!x) return;
    travIn_R(x->lChild, visit);
    visit(x->data);
    travIn_R(x->rChild, visit);
}

3.2 迭代版

#版本1

template <typename T> //从当前节点出发，沿左分支不断深入，直至没有左分支的节点
static void goAlongLeftBranch(BinNodePosi(T) x, Stack<BinNodePosi(T)>& S) {
    while (x) { S.push(x); x = x->lChild; } //当前节点入栈后随即向左侧分支深入，迭代直到无左孩子
}

template <typename T, typename VST> //元素类型、操作器
void travIn_I1(BinNodePosi(T) x, VST& visit) { //二叉树中序遍历算法（迭代版#1）
    Stack<BinNodePosi(T)> S; //辅助栈
    while (true) {
        goAlongLeftBranch(x, S); //从当前节点出发，逐批入栈
        if (S.empty()) break; //直至所有节点处理完毕
        x = S.pop(); visit(x->data); //弹出栈顶节点幵讵问之
        x = x->rChild; //转向右子树
    }
}

#版本2

版本1的等价形式，只是更简明。
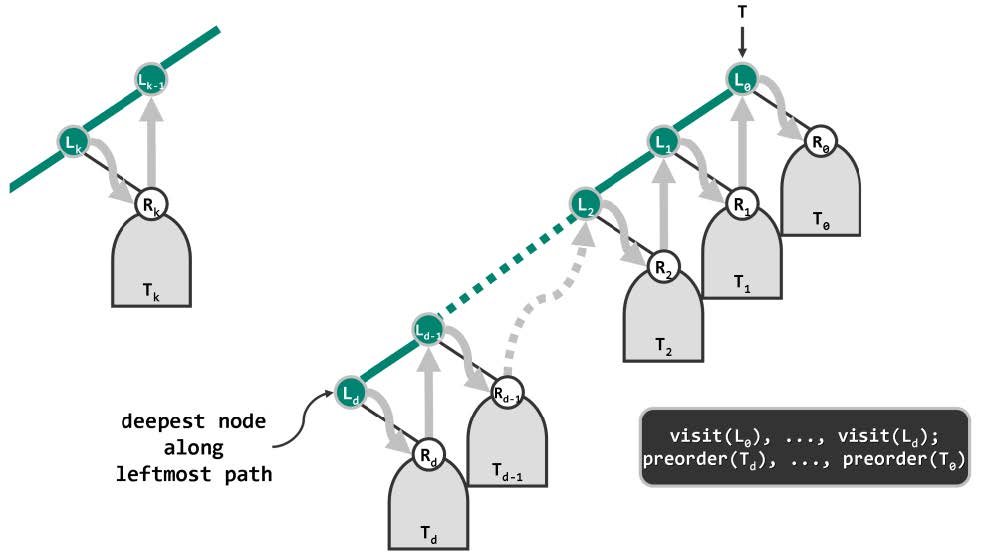
版本1和版本2的思路示意：

template <typename T, typename VST> //元素类型、操作器
void travIn_I2(BinNodePosi(T) x, VST& visit) { //二叉树中序遍历算法（迭代版#2）
    Stack<BinNodePosi(T)> S; //辅助栈
    while (true)
        if (x) {
            S.push(x); //根节点进栈
            x = x->lChild; //深入遍历左子树
        } else if (!S.empty()) {
            x = S.pop(); //尚未访问的最低祖先节点退栈
            visit(x->data); //访问该祖先节点
            x = x->rChild; //遍历祖先的右子树
        } else
            break; //遍历完成
}

#版本3

无须辅助栈，辅助空间仅O(1)，就地算法。

template <typename T, typename VST> //元素类型、操作器
void travIn_I3(BinNodePosi(T) x, VST& visit) { //二叉树中序遍历算法（迭代版#3，无需辅助栈）
    bool backtrack = false; //前一步是否刚从右子树回溯——省去栈，仅O(1)辅助空间
    while (true)
        if (!backtrack && HasLChild(*x)) //若有左子树且不是刚刚回溯，则
            x = x->lChild; //深入遍历左子树
        else { //否则——无左子树或刚刚回溯（相当于无左子树）
            visit(x->data); //访问该节点
            if (HasRChild(*x)) { //若其右子树非空，则
                x = x->rChild; //深入右子树继续遍历
                backtrack = false; //并关闭回溯标志
            } else { //若右子树空，则
                if (!(x = x->succ())) break; //回溯（含抵达末节点时的退出返回）
                backtrack = true; //并讴置回溯标志
            }
        }
}

4. 后序遍历

4.1 递归式

template <typename T, typename VST> //元素类型、操作器
void travPost_R(BinNodePosi(T) x, VST& visit) { //二叉树后序遍历算法（递归版）
    if (!x) return;
    travPost_R(x->lChild, visit);
    travPost_R(x->rChild, visit);
    visit(x->data);
}

4.2 迭代式

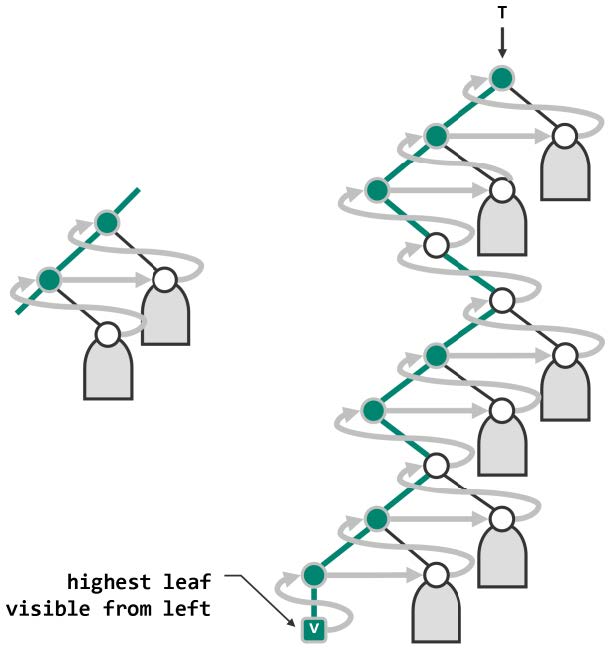
template <typename T> //在以S栈顶节点为根的子树中，找刡最高左侧可见叶节点
static void gotoHLVFL(Stack<BinNodePosi(T)>& S) { //沿递所遇节点依次入栈
    while (BinNodePosi(T) x = S.top()) //自顶而下，反复检查当前节点（即栈顶）
    if (HasLChild(*x)) { //尽可能向左
        if (HasRChild(*x)) S.push(x->rChild); //若有右孩子，优先入栈
        S.push(x->lChild); //然后才转至左孩子
    } else //实不得已
        S.push(x->rChild); //才向右
    S.pop(); //迒回之前，弹出栈顶的空节点
}

template <typename T, typename VST>
void travPost_I(BinNodePosi(T) x, VST& visit) { //二叉树的后序遍历（迭代版）
    Stack<BinNodePosi(T)> S; //辅助栈
    if (x) S.push(x); //根节点入栈
    while (!S.empty()) {
        if (S.top() != x->parent) //若栈顶非当前节点之父（则必为其右兄），此时需
            gotoHLVFL(S); //在以其右兄为根之子树中，找到HLVFL（相当于递归深入其中）
        x = S.pop(); visit(x->data); //弹出栈顶（即前一节点之后继），并讵问之
    }
}

5. 层次遍历

不同于迭代式的先序、中序、后序遍历使用辅助栈，层次遍历使用的是辅助队列。

template <typename T> template <typename VST> //元素类型、操作器
void BinNode<T>::travLevel(VST& visit) { //二叉树层次遍历算法
    Queue<BinNodePosi(T)> Q; //辅助队列
    Q.enqueue(this); //根节点入队
    while (!Q.empty()) { //在队列再次变空之前，反复迭代
        BinNodePosi(T) x = Q.dequeue(); visit(x->data); //取出队首节点并访问之
        if (HasLChild(*x)) Q.enqueue(x->lChild); //左孩子入队
        if (HasRChild(*x)) Q.enqueue(x->rChild); //右孩子入队
    }
}

6. 二叉树的重构

问题描述：已知由任何一棵二叉树，都可导出其三个遍历序列：preorder, inorder, postorder。那么，若已知某二叉树的遍历序列，可否还原出其拓扑结构呢？

结论——如下条件下，可还原一棵二叉树:

注：此法好像需要二叉树中不能有数值重复的节点（据《剑指offer》P.195）

条件	图示
[先序\|后序]+中序
[先序 + 后序] × 真二叉树

二叉树

详情