图

1. BFS

广度优先遍历(breadth-first search, BFS)。

1.1 算法实现

既然二叉树的层次遍历就是BFS，那么对于真正的图的BFS算法引入辅助队列也就不足为奇了。

当然，与树不同的是，图中每个顶点都有一个状态特征。

/******************************************************************************************
 * Data Structures in C++
 * ISBN: 7-302-33064-6 & 7-302-33065-3 & 7-302-29652-2 & 7-302-26883-3
 * Junhui DENG, deng@tsinghua.edu.cn
 * Computer Science & Technology, Tsinghua University
 * Copyright (c) 2003-2019. All rights reserved.
 ******************************************************************************************/

template <typename Tv, typename Te> //广度优先搜索BFS算法（全图）
void Graph<Tv, Te>::bfs ( int s ) { //assert: 0 <= s < n
   reset(); int clock = 0; int v = s; //初始化
   do //逐一检查所有顶点
      if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
         BFS ( v, clock ); //即从该顶点出发启动一次BFS
   while ( s != ( v = ( ++v % n ) ) ); //按序号检查，故不漏不重
}

template <typename Tv, typename Te> //广度优先搜索BFS算法（单个连通域）
void Graph<Tv, Te>::BFS ( int v, int& clock ) { //assert: 0 <= v < n
   Queue<int> Q; //引入辅助队列
   status ( v ) = DISCOVERED; Q.enqueue ( v ); //初始化起点
   while ( !Q.empty() ) { //在Q变空之前，不断
      int v = Q.dequeue(); dTime ( v ) = ++clock; //取出队首顶点v
      for ( int u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u
         if ( UNDISCOVERED == status ( u ) ) { //若u尚未被发现，则
            status ( u ) = DISCOVERED; Q.enqueue ( u ); //发现该顶点
            type ( v, u ) = TREE; parent ( u ) = v; //引入树边拓展支撑树
         } else { //若u已被发现，或者甚至已访问完毕，则
            type ( v, u ) = CROSS; //将(v, u)归类于跨边
         }
      status ( v ) = VISITED; //至此，当前顶点访问完毕
   }
}

1.2 BFS的应用

连接域分解问题

......

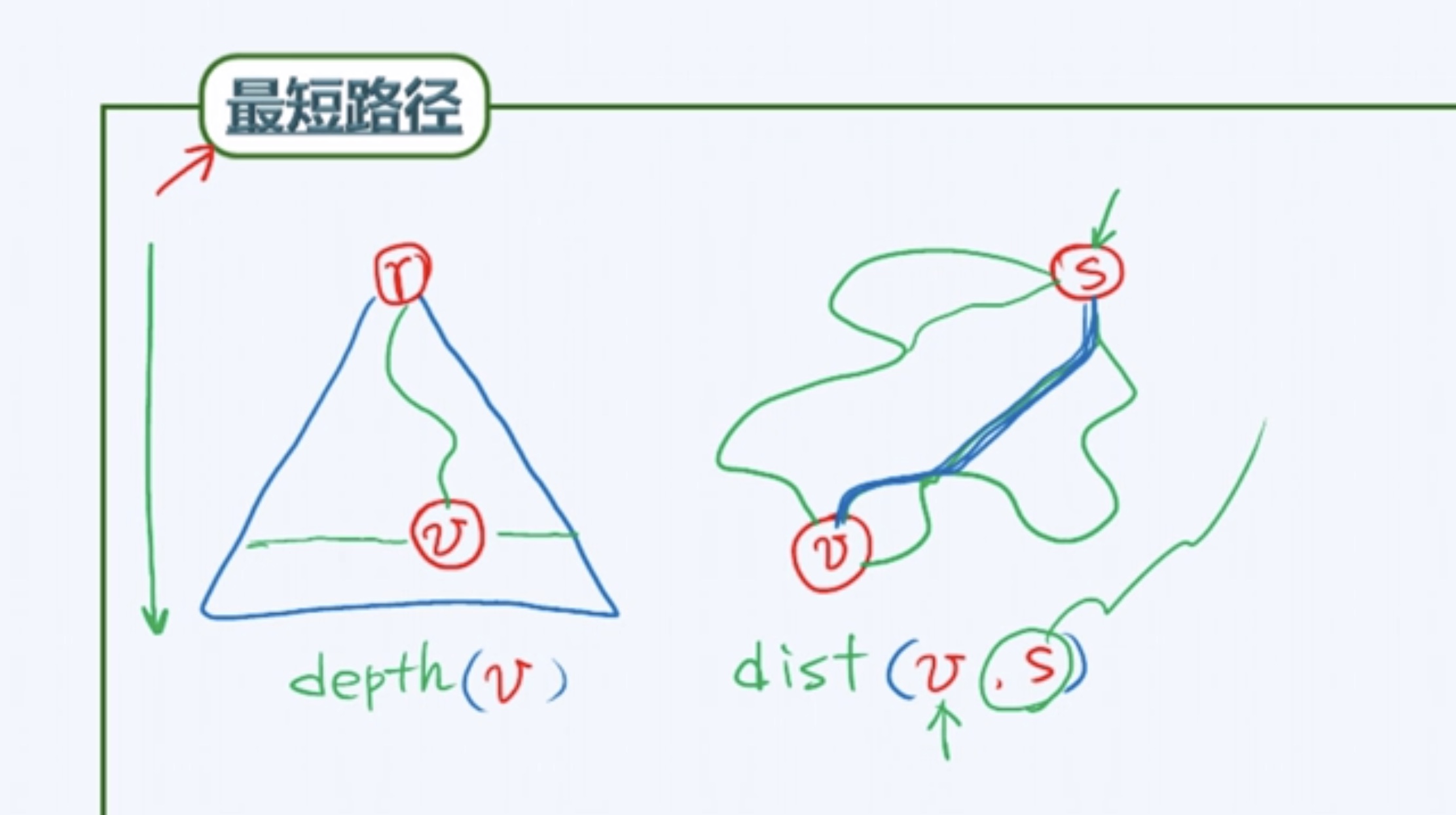
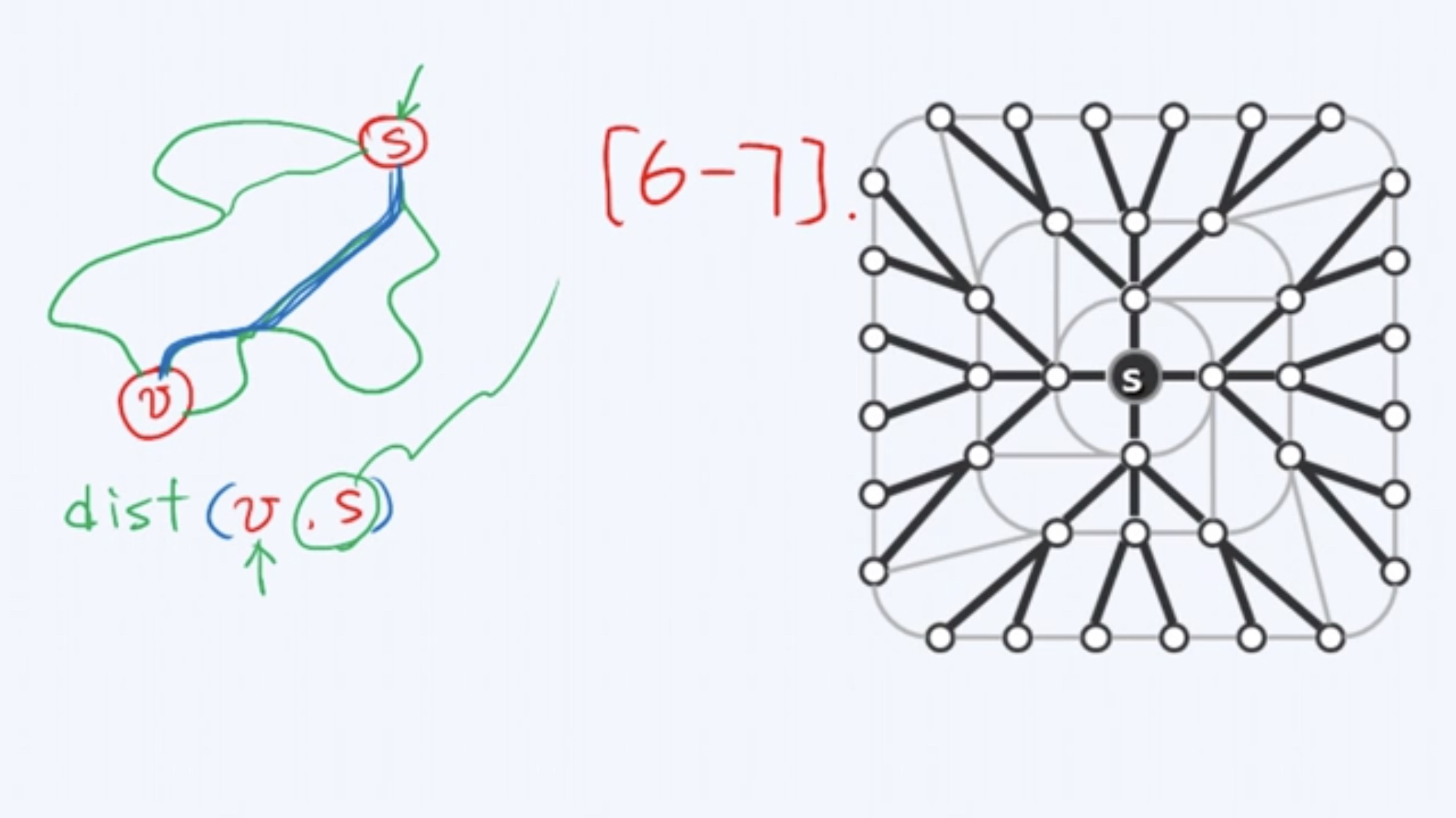
最短路径问题

应该指出，如果你真正熟悉了BFS的原理，将BFS应用于最短路径问题是再自然不过的事情。

2. DFS

深度优先遍历(deep-first traverse, DFS)

2.1 算法实现

递归版

/******************************************************************************************
 * Data Structures in C++
 * ISBN: 7-302-33064-6 & 7-302-33065-3 & 7-302-29652-2 & 7-302-26883-3
 * Junhui DENG, deng@tsinghua.edu.cn
 * Computer Science & Technology, Tsinghua University
 * Copyright (c) 2003-2019. All rights reserved.
 ******************************************************************************************/

template <typename Tv, typename Te> //深度优先搜索DFS算法（全图）
void Graph<Tv, Te>::dfs ( int s ) { //assert: 0 <= s < n
   reset(); int clock = 0; int v = s; //初始化
   do //逐一检查所有顶点
      if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
         DFS ( v, clock ); //即从该顶点出发启动一次DFS
   while ( s != ( v = ( ++v % n ) ) ); //按序号检查，故不漏不重
}

template <typename Tv, typename Te> //深度优先搜索DFS算法（单个连通域）
void Graph<Tv, Te>::DFS ( int v, int& clock ) { //assert: 0 <= v < n
   dTime ( v ) = ++clock; status ( v ) = DISCOVERED; //发现当前顶点v
   for ( int u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u
      switch ( status ( u ) ) { //并视其状态分别处理
         case UNDISCOVERED: //u尚未发现，意味着支撑树可在此拓展
            type ( v, u ) = TREE; parent ( u ) = v; DFS ( u, clock ); break;
         case DISCOVERED: //u已被发现但尚未访问完毕，应属被后代指向的祖先
            type ( v, u ) = BACKWARD; break;
         default: //u已访问完毕（VISITED，有向图），则视承袭关系分为前向边或跨边
            type ( v, u ) = ( dTime ( v ) < dTime ( u ) ) ? FORWARD : CROSS; break;
      }
   status ( v ) = VISITED; fTime ( v ) = ++clock; //至此，当前顶点v方告访问完毕
}

迭代版

通过引入栈结构，动态记录从起始顶点s到当前顶点之间通路上的各个顶点，其中栈顶对应于当前顶点。 每当遇到处于UNDISCOVERED状态的顶点，则将其转换为DISCOVERED状态，并令其入栈； 一旦当前顶点的所有邻居都不再处于UNDISCOVERED状态，则将其转为VISITED状态，并令其出栈。

// Waiting for you...

2.2 DFS的应用

DFS无疑是最为重要的图遍历算法。基于DFS的的框架，可以导出和建立大量的图算法。

拓扑排序

双连通域分解