对一幅输入图像f(x,y)进行处理,得到一幅退化后的图像g(x,y);给定退化函数H以及加性噪声项η(x,y)的一些知识后,图像复原的目的就是获得原始图像的一个估计f~(x,y)。
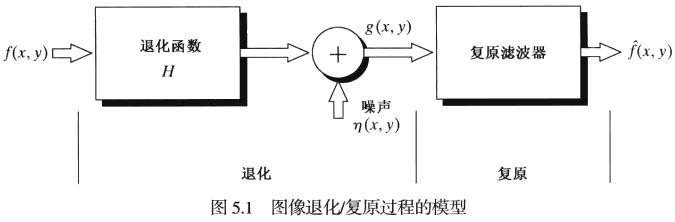
如果H是一个线性的、位置不变的过程,退化为:
| 空间域中的退化 | 频率域中的退化 |
|---|
| g(x,y)=h(x,y)⊛f(x,y)+η(x,y) | G(μ,v)=H(μ,v)F(μ,v)+N(μ,v) |
噪声的空间特性是指噪声是否与图像相关;噪声的频率特性是指傅里叶域中噪声的频率内容,即相对于电磁波谱的频率。
除周期噪声外,本章中讨论的所有噪声均假设与空间坐标无关,且噪声与图像本身不相关(即像素值与噪声成分的值之间不相关)。
所谓周期噪声是在图像获取期间由电力或机电干扰产生的,是一种空间相关噪声,可通过频率域滤波来显著地减少。周期噪声的参数通常通过检测图像的傅里叶谱来估计,其趋向于产生频率尖峰。
当噪声的傅里叶谱是常量时,称为白噪声。
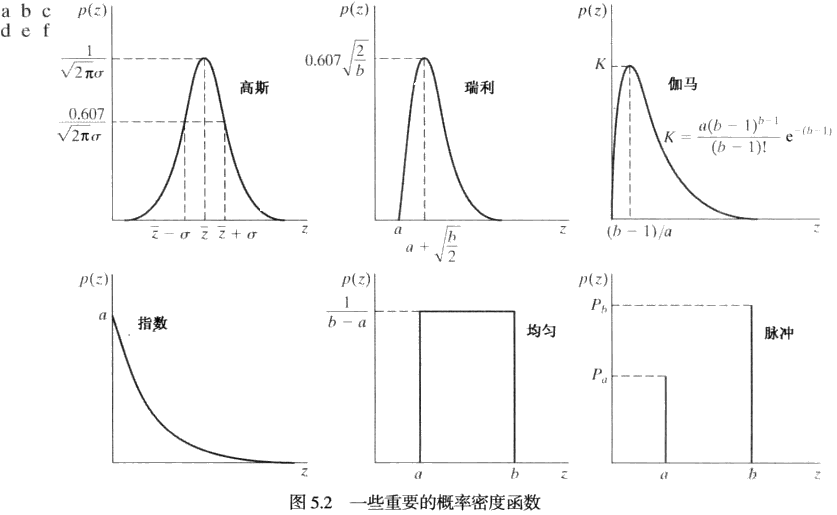
我们关心的是噪声成分η(x,y)中灰度值的统计特性,可以认为噪声是由概率密度函数表征的随机变量,以z表示灰度值,表示zˉz 的均值,σ表示z的标准差。常见噪声概率密度函数有:
 |  |
|---|
高斯噪声
p(z)=2πσ1e−(z−zˉ)2/2σ2
瑞利噪声
p(z)={b2(z−a)e−(z−a)2/b,0,z⩾az<azˉ=a+πb/4σ2=4b(4−π)
伽马噪声
p(z)={(b−1)!abzb−1e−az,0,z⩾az<azˉ=abσ2=a2b
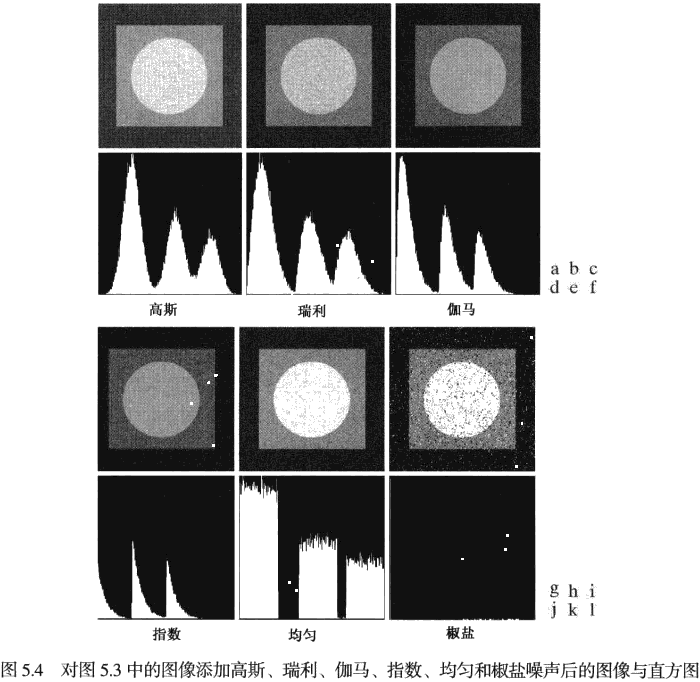
指数噪声
p(z)={(b−1)!abzb−1e−az,0,z⩾az<azˉ=abσ2=a2b
均匀噪声
p(z)={b−a1,0a⩽z⩽b the others zˉ=2a+bσ2=12(b−a)2
脉冲(椒盐)噪声
p(z)=⎩⎨⎧Pa,Pb,1−Pa−Pb,z=az=b the others
当一幅图像中唯一存在的退化是噪声时,复原变为:
| 空间域 | 频率域 |
|---|
| g(x,y)=f(x,y)+η(x,y) | G(μ,v)=F(μ,v)+N(μ,v) |
由于噪声项未知,从g(x,y)或G(μ,v)中送去它们不现实。在仅存在加性噪声的情况下,可以选择空间滤波方法如下:
其中自适应滤波器的性能要优于其他所有滤波器,但代价是复杂度提高了。
- 均值滤波器
- 算术均值滤波器:平滑一幅图像中的局部变化,虽然模糊了结果,但降低了噪声
- 几何均值滤波器:其平滑效果可与算术均值相比较,但丢失了更少的图像细节
- 谐波均值滤波器:关于处理高斯噪声这样的噪声,对于盐粒噪声效果较好,不适于胡椒噪声
- 逆谐波均值滤波器:适合减少或消除椒盐噪声的影响
- 统计排序滤波器
- 中值滤波器
- 最大值滤波器:对于发现图像中的最亮点非常有用
- 最小值滤波器:对于发现图像中的最暗点非常有用
- 中点滤波器:最适用于处理随机分布的噪声,如高斯或均匀噪声
- 修正的阿尔法均值滤波器:在包括多种噪声的情况下很有用,如混合有高斯和椒盐噪声的情况
- 自适应滤波器
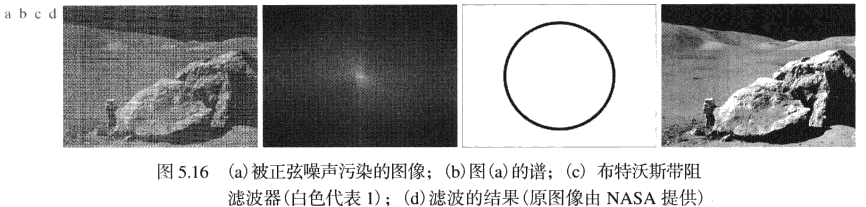
用频率域技术可有效地消除周期噪声的基本原理是,在傅里叶变换中,周期噪声在对应于周期干扰的频率处以集中的能量脉冲形式出现,可用一个选择性滤波器将其分离。
带阻滤波器
带通滤波器
陷波滤波器
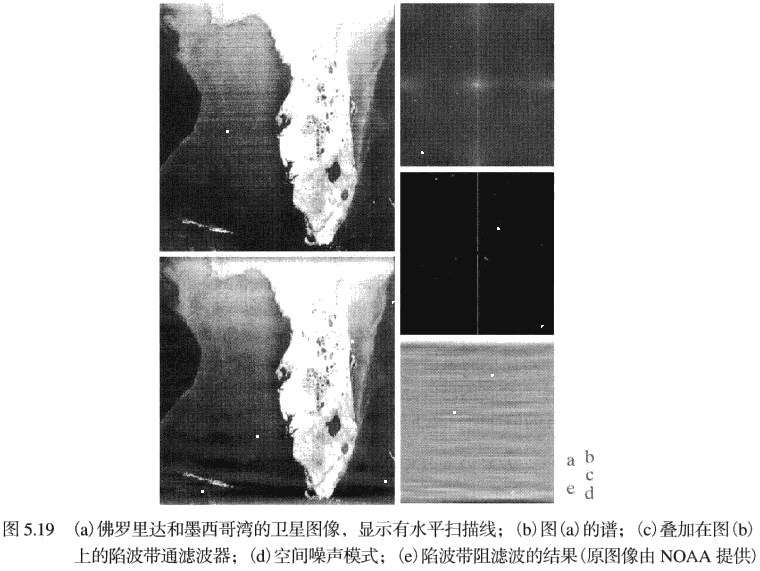
最佳陷波滤波器
在图像复原时,主要有 3 种用于估计退化函数的方法:观察法、试验法、数学建模法。
使用某种方法估计的退化函数来复原一幅图像的过程,有时称为盲去卷积,因为真正的退化函数很难完全知晓。





