彩色图像处理
彩色基础
彩色图像处理可分为两个主要领域：全彩色处理和伪彩色处理。在全彩色处理中，通常要求图像用全彩色传感器获取，如彩色电视摄像机或彩色扫描仪；在伪彩色处理中，问题是对一种特定的单色灰度或灰度范围赋予一种颜色。
利用彩色的动力之一是人类可以辨别几千种色调和强度，而相比之下只能辨别 20 多种灰度。
彩色光大约覆盖电磁波谱中 400~700 nm 的范围，描述彩色光源质量的 3 个基本量是辐射、光强和亮度。
由远红外波谱范围的光源发出的光，可能具有很大的辐射，但观察者却很难感知到它；它的光强几乎是零。
- 辐射：从光源流出的能量的总和，通常用瓦特（W）来度量
- 光强：用流明来度量，它给出观察者从光源感知的能量总和的度量
- 亮度：是一个主观描绘子，实际上不可度量。亮度体现了无色的强度的概念，是描述色彩感觉的一个关键因素
为标准化起见，CIE（国际照明委员会）于 1931 年指定了特定波长值为三原色：蓝色=435.8nm，绿色=546.1nm，红色=700nm：
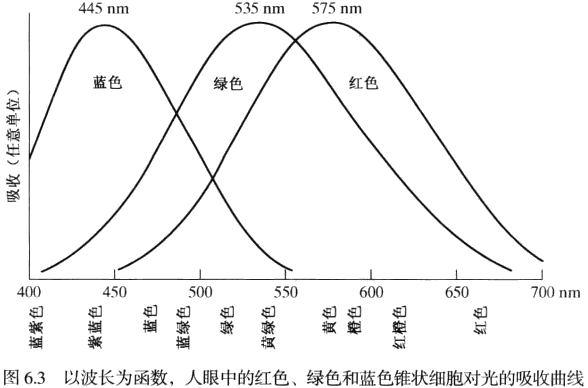
通常用以区别不同颜色特性的是亮度、色调和饱和度，色调与饱和度一起称为色度：
- 亮度：如上，亮度表达了无色的强度概念
- 色调：光波混合中与主波长有关的属性，表示观察者感知的主要颜色。当我们说一个物体是红色、橙色或黄色时，指的是其色调
- 饱和度：指相对纯净度，或一种颜色混合白光的数量。纯谱色是全饱和的，如深红色（红加白）、淡紫色（紫加白）这样的彩色是欠饱和的。饱和度与所加白光的数量成反比。
彩色模型
彩色模型的目的是，在某些标准下用通常可以接受的方式方便地对彩色加以说明。
RGB 模型——在 RGB 模型中，基于笛卡尔坐标系，每种颜色由红、绿、蓝三种维度的分量组成的向量表示，黑点位于原点处，白色位于离原点最远的角上。
- 在 RGB 模型中，灰色点（RGB 值相等的点）沿着原点出发的对角线从黑色延伸到白色。
- RGB 彩色模型表示的图像由 3 个分量图像组成，每种颜色一幅分量图像。当送入 RGB 监视器时，这 3 幅图像在屏幕上混合生成一幅合成的彩色图像。
- 在 RGB 模型中，表示每个像素的比特数称为像素深度。若一幅 RGB 图像中每幅红、绿、蓝图像都是一幅 8 比特图像，则可以说每个 RGB 彩色像素（即(R,G,B)值的三元组）有 24 比特的深度，术语全彩色图像通常用来表示一幅 24 比特的 RGB 彩色图像，24 比特的 RGB 图像中拥有的颜色总数是$(28)3=16777216$。
其他彩色模型有 CMY/CMYK 彩色模型、HSI 彩色模型等。详见 P.257。
伪彩色/全彩色图像处理
伪彩色图像处理是指基于一种指定的规则对灰度值赋以颜色的处理，伪彩色主要用于人目视观察和解释单幅图像或序列图像中的灰度级事件。
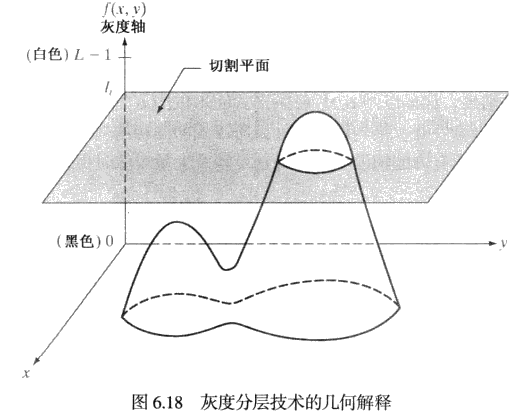
灰度分层和彩色编码技术是伪彩色图像处理的最简单的例子之一。
灰度分层技术：令$[0,L−1]$表示灰度级，令$l_0$ 代表黑色（$f(x,y)=0$），并令$l_{L−1}$ 代表白色（$f(x,y)=L−1$），假定垂直于灰度轴的$P$个平面定义为灰度级$l_1,l_2,…,l_P,0<P<L−1$，则$P$个平面将灰度分为$P+1$个区间$V_1,V_2,…,V_{P+1}$ 。灰度级到彩色赋值的关系为$f(x,y)=c_k\quad f(x,y)∈V_k$，其中$c_k$ 是与第$k$个灰度区间$V_k$ 有关的颜色，$V_k$ 由位于$l=k−1$和$l=k$处的分割平面定义。
 |  |
|---|
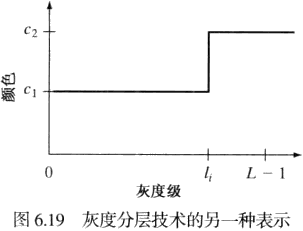全彩色图像处理方法分为两大类，第一类是分别处理每一幅分量图像，然后由分别处理过的分量图像来形成一幅处理过的合成彩色图像，第二类是直接处理彩色像素，彩色像素实际上是向量。
令$c$代表 RGB 彩色空间中的一个任意向量，$c$的分量即彩色分量是坐标$(x,y)$的函数，故可如下表示：
$$ c(x, y)=\left[\begin{array}{l}c_{R}(x, y) \ c_{G}(x, y) \ c_{B}(x, y)\end{array}\right]=\left[\begin{array}{l}R(x, y) \ G(x, y) \ B(x, y)\end{array}\right] $$
根据像素是彩色像素因而是个向量的事实，单个彩色分量处理的结果并不总是等同于彩色向量空间中的直接处理。如单独对彩色图像的分量进行直方图均衡通常是不明智的，这将产生不正确的彩色。一种合乎逻辑的方法是均匀地展开这种彩色灰度，而保持彩色本身（即色调）不变。
每种彩色分量的处理要等同于基于向量的处理必须满足两个条件：
- 处理必须对向量和标量都可用；
- 对向量的每个分量的操作对于其他分量必须是独立的。
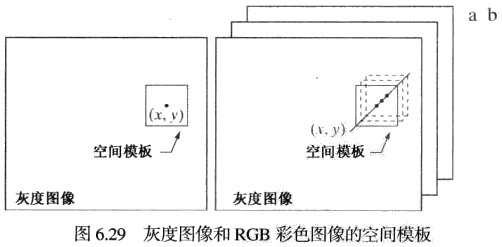
彩色图像的平滑和锐化——令$S_{xy}$ 表示中心位于$(x,y)$的邻域定义的一组坐标，在该邻域中 RGB 分量的向量平均值为$\bar{\bold{c}}(x,y)$；向量 c 的拉普拉斯变换为$\nabla^2[\bold{c}(x,y)]$。
平滑
$$ \overline{\boldsymbol{c}}(x, y)=\frac{1}{K} \sum_{(s, t) \in S_{x y}} \boldsymbol{c}(s, t)=\left[\begin{array}{l}\frac{1}{K} \sum_{(s, t) \in S_{x y}} R(s, t) \ \frac{1}{K} \sum_{(s, t) \in S_{x y}} G(s, t) \ \frac{1}{K} \sum_{(s, t) \in S_{x y}} B(s, t)\end{array}\right] $$
锐化 $$ \nabla^{2}[c(x, y)]=\left[\begin{array}{l} \nabla^{2} R(x, y) \ \nabla^{2} G(x, y) \ \nabla^{2} B(x, y) \end{array}\right] $$
通常，彩色图像的噪声内容在每个彩色通道中具有相同的特性，但噪声对不同彩色通道所造成的影响不同。