空间域处理

1. 综述

空间域处理主要分为灰度变换和空间滤波两类。

1. 灰度变换对图像的单个像素进行操作，主要以对比度和阈值处理为目的

2. 空间滤波主要为改善性能，如通过图像中每个像素的邻域处理来锐化图像

通常，空间域技术在执行上更有效，且执行所需的处理资源较少。本章讨论的空间域处理可表示为下式：

$$g(x,y)=T[f(x,y)]$$

其中，$f(x,y)$是输入图像，$g(x,y)$是处理后的图像，$T$是在点$(x,y)$的邻域上定义的关于 $f$ 的一种算子。当该邻域位于图像的边界上时，部分邻域将位于图像的外部，此时，可令$T$在做指定的计算时忽略外侧邻点，或用$0$或其他指定的灰度值填充图像的边缘。

2. 灰度变换

对于$g(x,y)=T[f(x,y)]$，最小邻域为$1×1$，此时$g$仅取决于点$(x, y)$处的$f$值，上述$T$则成为如下的灰度变换函数，例子如下右图：

$s=T(r)$

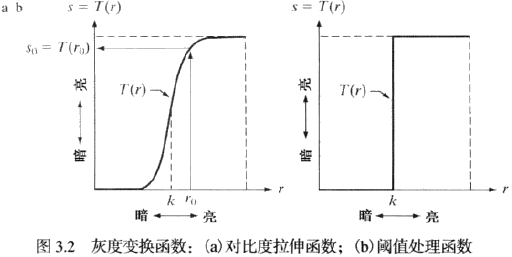2.1 灰度变换函数

一些基本的灰度变换函数：

• 反转变换：$s=L−1−r$

• 对数变换：$s=c \log (1+r)$

• 幂律变换/伽马变换：$s=cr^γ$

• 分段线性变换函数：

  • 对比度拉伸：扩展图像灰度级动态范围

    

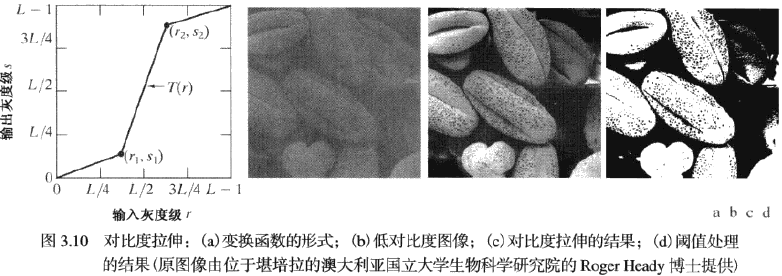
  • 灰度级分层：突出图像中特定灰度范围的亮度以增强某些特征，如卫星图像中的水体和 X 射线图像中的缺陷

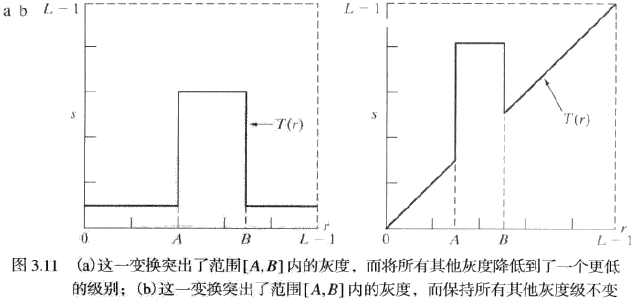
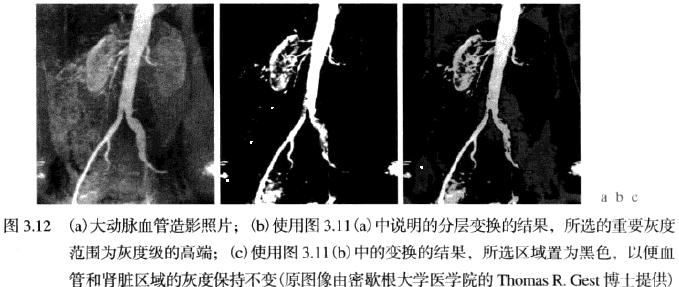
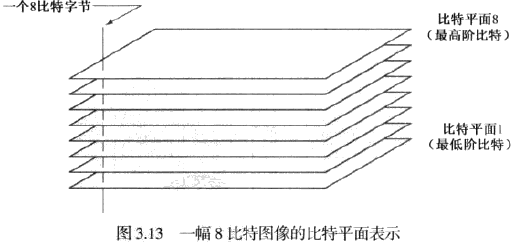
  • 比特平面分层：替代突然灰度级范围，可突出特定比特来突出整个图像的外观。根据灰度变换函数，显示一幅 8 比特图像的第 8 个比特平面并不困难，可用阈值灰度变换函数处理输入图像得到二值图像，该函数将$0\sim127$之间的所有灰度映射为 0，而将$128\sim255$之间的所有灰度映射为 1.

2.2 直方图

直方图处理：灰度级范围为$[0, L−1]$的数字图像的直方图是离散函数$h(r_k )=n_k$，其中$r_k$ 是第$k$级灰度值，$n_k$ 是图像中灰度为$r_k$ 的像素个数。

图像直方图的一些特征

1. 在暗图像中，直方图的分量集中在灰度级的低（暗）端；亮图像中直方图的分量则倾向于灰度级的高端

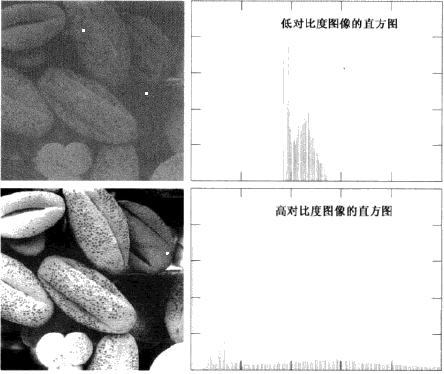
2. 低对比度图像具有较窄的直方图，且集中灰度级的中部。对于单色图像，这意味着暗淡，好像灰度被冲淡了一样

3. 高对比度图像中直方图的分量覆盖了很宽的灰度级范围，且像素的分布没有太不均匀，只有少量垂线比其他的高许多

4. 直观上有如下结论：如一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀，则该图像会有高对比度的外观并展示灰色调的较大变化，最终效果将是一幅灰度细节丰富且动态范围较大的图像

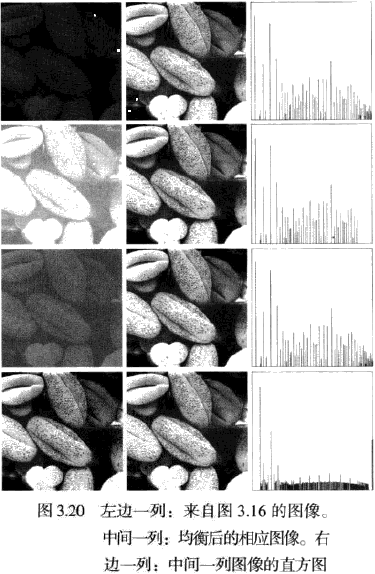
直方图均衡/直方图线性变换：以$r_k$ 为输入图像的第 k 级灰度值，直方图均衡变换$T(r_k )$如下，其逆变换表示为$r_k=T^{−1}(s_k)$。直方图均衡的变换函数是确定的，该函数寻求产生有均匀直方图的输出图像，处理后的图像灰度级会跨越更宽的灰度级范围，最终结果是增强了对比度。

$s_{k}=T\left(r_{k}\right)=(L-1) \sum_{j=0}^{k} p_{r}\left(r_{j}\right)=\frac{L-1}{M N} \sum_{j=0}^{k} n_{j}, k=0,1,2, \ldots, L-1$

直方图规定化/直方图匹配：对于某些应用，采用直方图均衡式的直方图的基本增强并不是最好的办法，有时我们希望处理后的图像具有规定的直方图形状。具体操作步骤可参见冈萨雷斯《数字图像处理》第三版 P.82。需要强调的是，直方图规定化在大多数时候都是试凑过程。

局部直方图处理：以图像中每个像素的领域中的灰度分布为基础设计变换函数。没啥好说的，参考 P.84。

3. 空间滤波基础

这里的滤波一词借用于频率域处理，实际上，线性空间滤波器与频率域滤波之间存在一一对应关系，然而空间滤波还可用于非线性滤波，这在频率域中是做不到的。

3.1 空间滤波器

空间滤波器也称为核、模板，由一个邻域（通常是一个较小的矩形）和对该邻域所包围像素执行的预定义操作组成。滤波产生一个新像素，新像素的坐标等于邻域中心的坐标，像素的值是滤波操作的结果。滤波器的中心访问输入图像中的每个像素后，就生成了滤波处理后的图像。如果在图像像素上执行的是线性操作，就称该滤波器为线性空间滤波器，否则，就称为非线性空间滤波器。

空间滤波器的基本类型有平滑空间滤波器与锐化空间滤波器。

3.2 相关与卷积

对于大小为$m×n$的模板，我们常常假设$m=2a+1, n=2b+1$，其中$a,b$为正整数，这意味着我们关注的是奇数尺寸的滤波器，其最小尺寸为$3×3$。一般地，使用大小为$m×n$的滤波器对小为$M×N$的图像进行线性空间滤波可表示为下式，其中$x$和$y$是可变的，以便$w$中每个像素可访问$f$中的每个像素，滤波器的响应$g(x,y)$是滤波器系数与对应图像像素的乘积之和（称为相关操作）。

$g(x, y)=\sum_{s=-a}^{a} \sum_{t=-b}^{b} w(s, t) f(x+s, y+t)$

相关是滤波器模板移过图像并计算每个位置乘积之和的处理；卷积的机理相似，但滤波器首先要旋转$180°$。注意这里的零填充不是唯一的选择。

离散单位冲激——包含单个 1 而其余都是 0 的矩阵（原话为函数，我 TM？？？）称为离散单位冲激。一个滤波器与离散单位冲激相关，会在该冲激的位置产生该滤波器的一个翻转版本；而一个滤波器与离散单位冲激卷积，得到的是在该冲激处的一个副本。

一维 ↓	二维 ↓

设有一个大小为$m×n$的滤波器$w(x,y)$与一幅图像$f(x,y)$，相关与卷积的公式表示分别为：

• 相关：

  $$w(x,y)⊙f(x,y)=\sum_{s=−a}^a\sum_{t=−b}^b{w(s,t)f(x+s,y+t)}$$

• 卷积：

  $$w(x,y)⊛f(x,y)=\sum_{s=−a}^a\sum_{t=−b}^b{w(s,t)f(x−s,y−t)}$$

3.3 平滑空间滤波器

平滑空间滤波器——用于模糊处理和降低噪声。模糊处理经常用于预处理任务中，例如在目标提取之前去除图像中的一些琐碎细节，以及连接直线或曲线的缝隙。

1. 均值滤波器——也叫平滑线性滤波器，其输出是包含在滤波器模板邻域内的像素的简单平均值。
2. 统计排序滤波器——也叫非线性空间滤波器，这种滤波器的响应以滤波器包围的图像区域中所包含的像素排序为基础，然后使用统计排序结果决定的值代替中心像素的值。
   1. 中值滤波器：最为知名，其用像素邻域内灰度的中值代替该像素的值，提供了
      1. 一种优秀的去噪能力，而且比同尺寸的均值滤波器的模糊程度明显要低
      2. 对处理脉冲噪声非常有效，脉冲噪声也叫椒盐噪声，其以黑白点的形式叠加在图像上
   2. 最大值滤波器：在搜寻一幅图像中的最亮点时非常有用
   3. 最小值滤波器：搜寻最暗点

3.4 锐化空间滤波器

锐化空间滤波器——锐化处理的主要目的是突出灰度的过滤部分，在逻辑上，锐化处理由空间微分来实现：

• 拉普拉斯算子——最简单的各向同性微分算子，所谓各向同性滤波器是指其响应是旋转不变的，即将原图旋转后进行滤波的响应结果与先对图像进行滤波之后再旋转的响应结果相同。

  • 二维图像的拉普拉斯算子

    $$\nabla^{2} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}$$

  • 离散形式的拉普拉斯算子

    $$\nabla^{2} f(x, y)=f(x+1, y)+f(x-1, y)+f(x, y+1)+f(x, y-1)-4 f(x, y)$$

  • 拉普拉斯增强图像的基本方法

    $$g(x, y)=f(x, y)+c\left[\nabla^{2} f(x, y)\right]$$

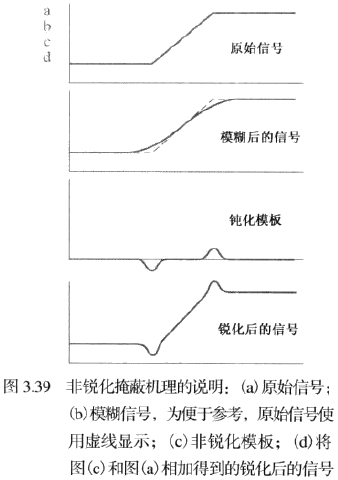
• 非锐化掩蔽与高提升滤波（参见 P.101）

  

• 使用一阶微分锐化（非线性）图像——梯度，相应有 Roberts 算子和 Sobel 算子