形态学图像处理
1. 预备知识
形态学及与其相关的数学概念,可从图像中提取表达和描绘区域形状的有用图像分量,如边界、骨架和凸壳等。本章介绍的形态学操作主要针对二值图像。
集合论
数学形态学的语言是集合论,数学形态学中的集合表示图像中的对象。
集合操作:在处理二值图像时,可以把图像想象为像素集合的前景(1 值)与背景(0 值)。此时若把区域定义为由前景像素组成,则下图所示的集合操作就变成了二值图像中目标坐标间的操作,OR、AND、和 NOT 这样的逻辑操作就是指普通的并、交和求补操作。

一个集合的反射表示为,平移表示为,其意义如下:
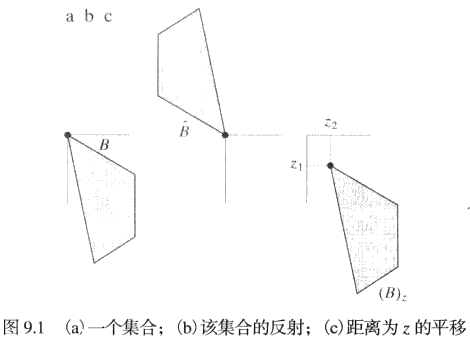
| 反射 | 平移 |
|---|---|
结构元
结构元(SE)——研究一幅图像中感兴趣特性所用的小集合或子图像。如下图,有:
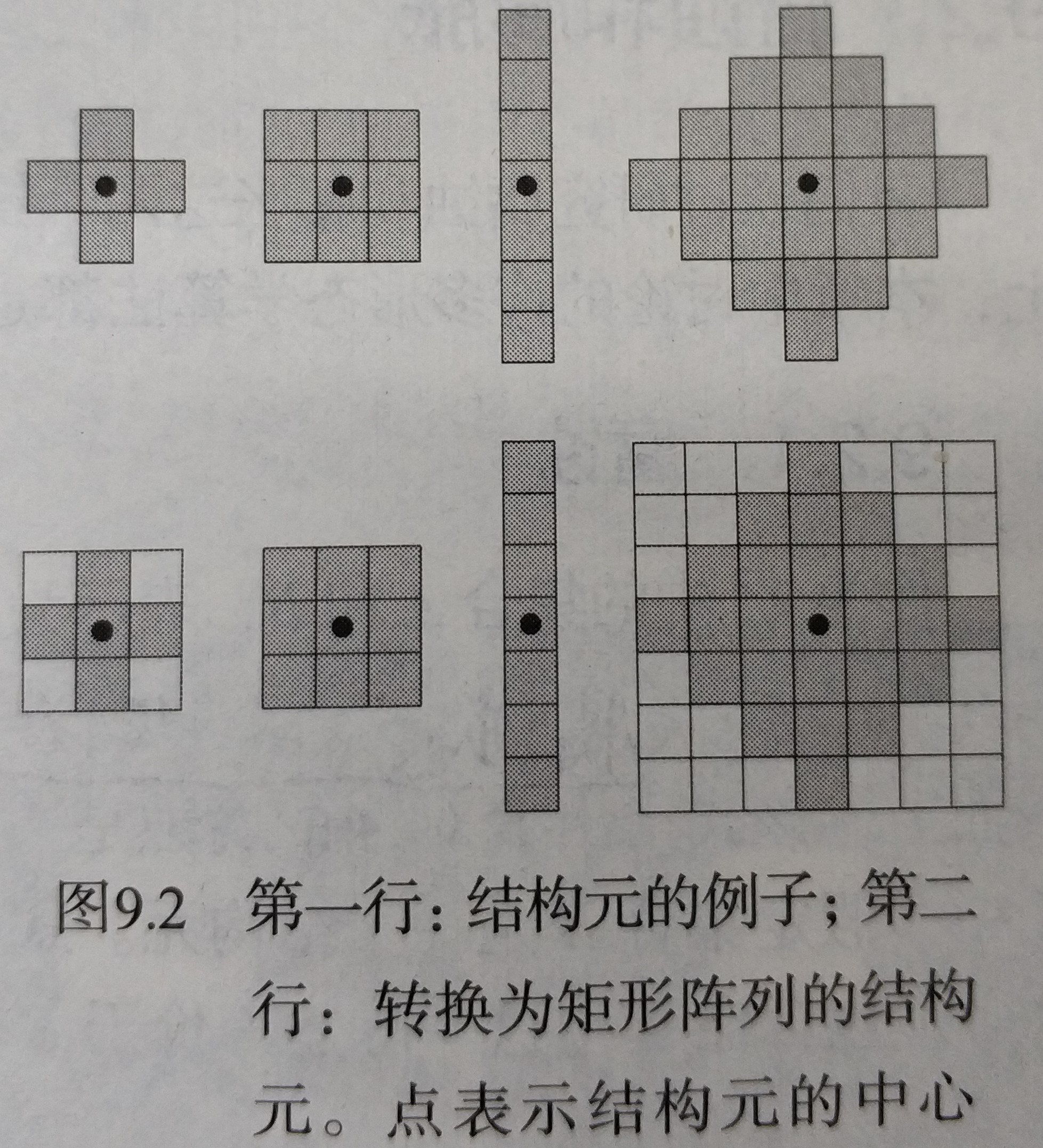
- SE 的成员用阴影的方块表示,此外还需指定结构元的原点,由黑点表示。
- 尽管一般情况下 SE 的中心在其重心处,但原点的选择取决于具体问题;当 SE 对称且未显示原点时,则假定其原点位于对称中心处。
- 对图像操作时,要求结构元是矩形阵列,常常通过添加最小可能数量的背景元素(非阴影部分)来形成矩阵,如第二行的第一个和最后一个 SE。
结构元的作用通常是用来处理一个其他的集合对象。如下图(a)、(b)分别示意的一个简单集合和一个结构元,当用计算机实现处理请求时要求用添加最小可能数量背景元素的方法把 A 也转化为一个矩形陈列,当结构元的原点位于原始集合的边界上时,背景边界要大到足以容纳整个结构元。
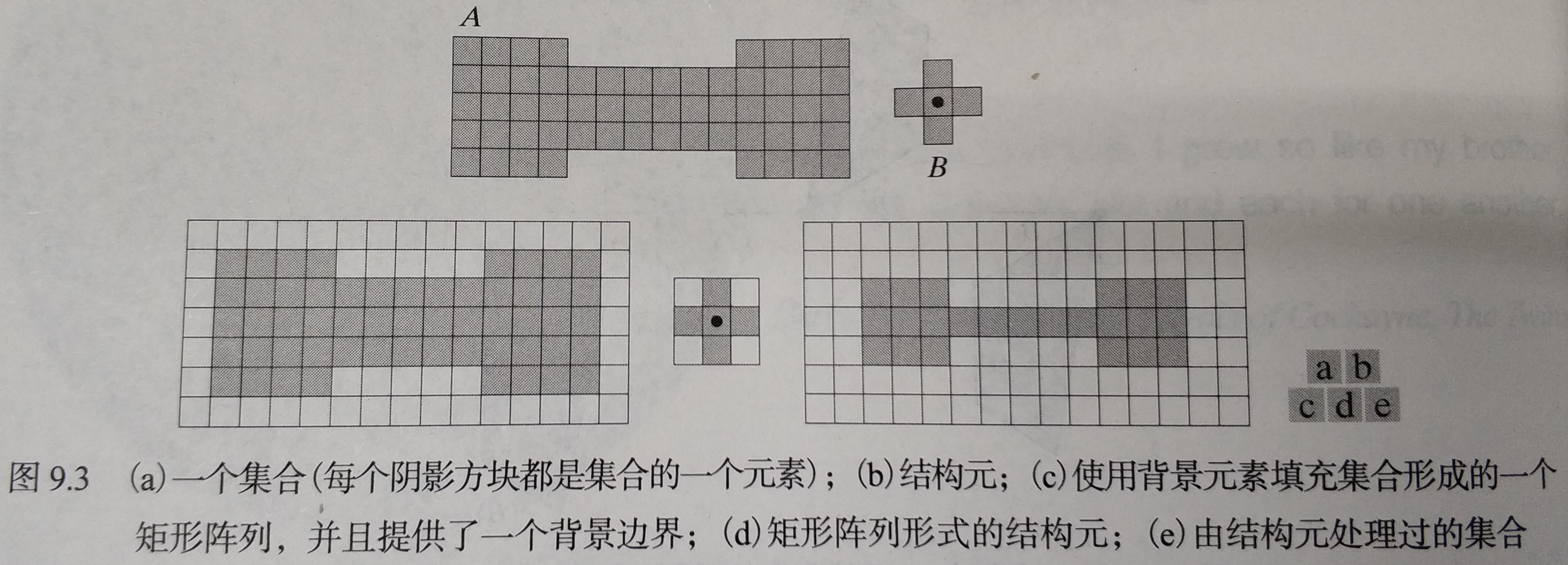 |
|---|
 |
2. 腐蚀和膨胀
许多形态学算法都是以腐蚀和膨胀这两种原始操作为基础的。
设有 中的集合和,以表示对的腐蚀,表示对的膨胀,有如下定义:
腐蚀:
表示 B 对 A 的腐蚀是一个用 z 平移的 B 包含在 A 中的所有的点 z 的集合。其等价定义为:
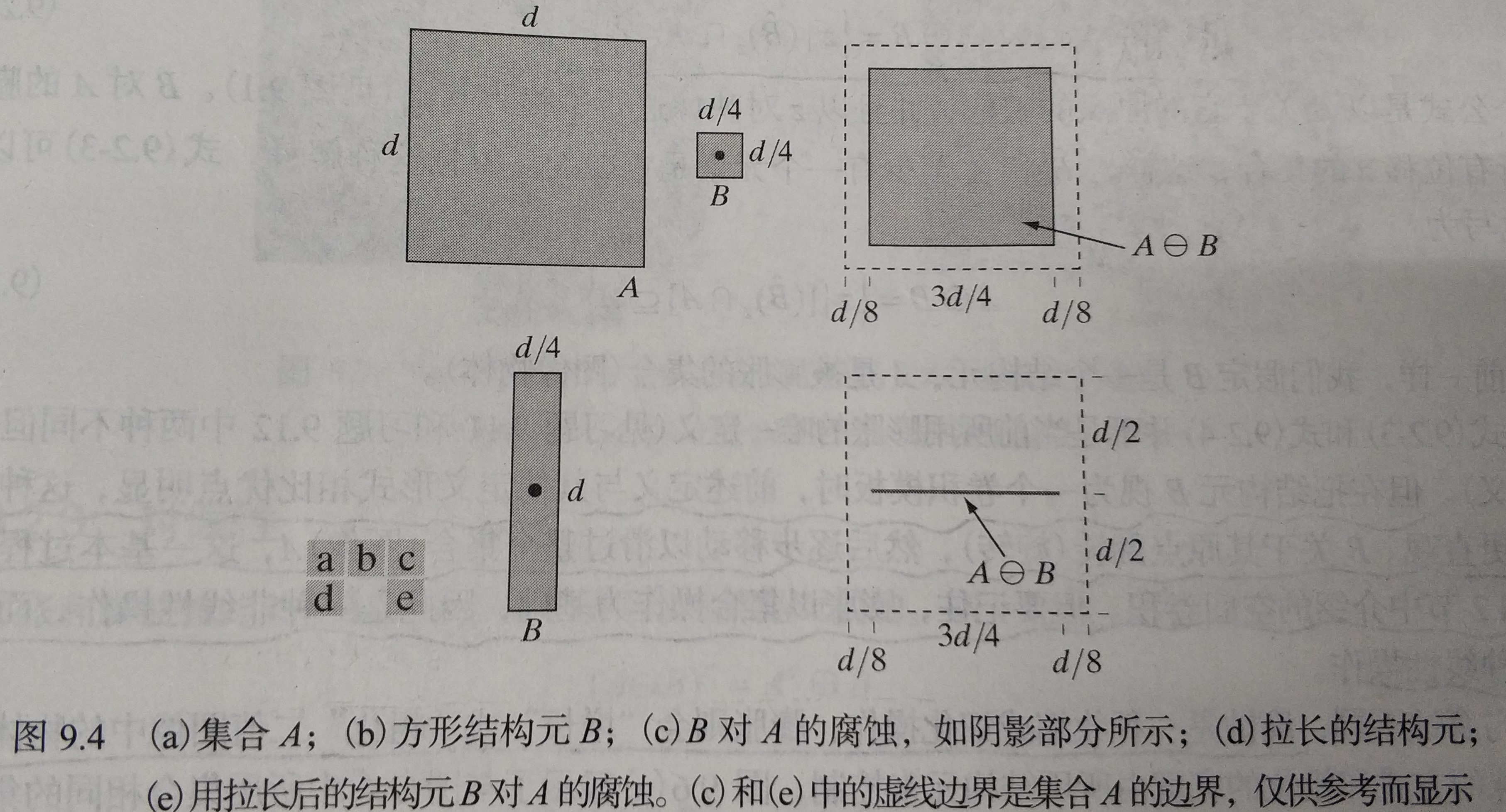
膨胀:
表示 B 关于原点反射,然后逐步滑动以滑过整个集合 A。其等价定义为:
腐蚀和膨胀的对比:
| 操作 | 作用 | 应用 |
|---|---|---|
| 腐蚀 | B 对 A 的腐蚀,可将结构元 B 视为一个空间模板 | 腐蚀是一种收缩或细化操作 |
| 膨胀 | B 对 A 的膨胀,可将结构元 B 视为一个卷积模板;但膨胀以集合操作为基础,故是一种非线性操作,而卷积是一种线性操作 | 膨胀则会增长或粗化二值图像中的物体 |
| 腐蚀-膨胀对偶性 | 当结构元关于其原点对称时,由于,可以用 B 对图像背景(即)进行膨胀,然后对结果求补即得到 B 对该图像腐蚀的结果 |
| 示图 | 说明 |
|---|---|
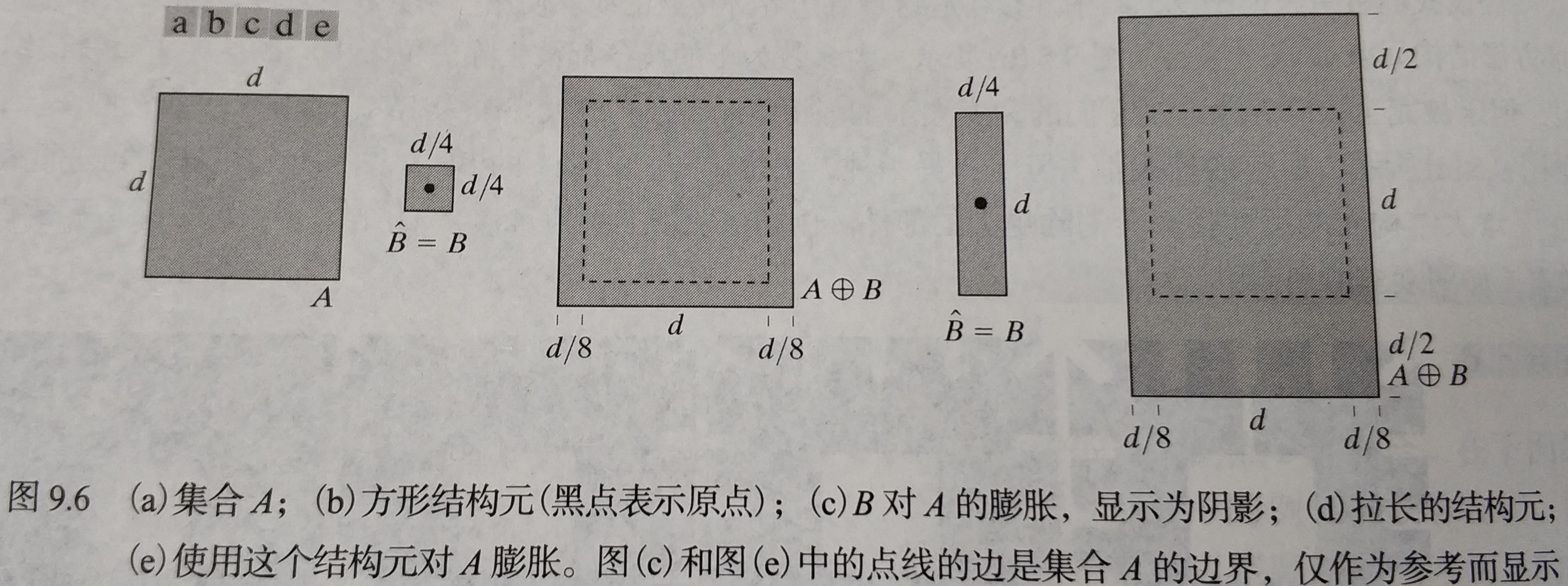
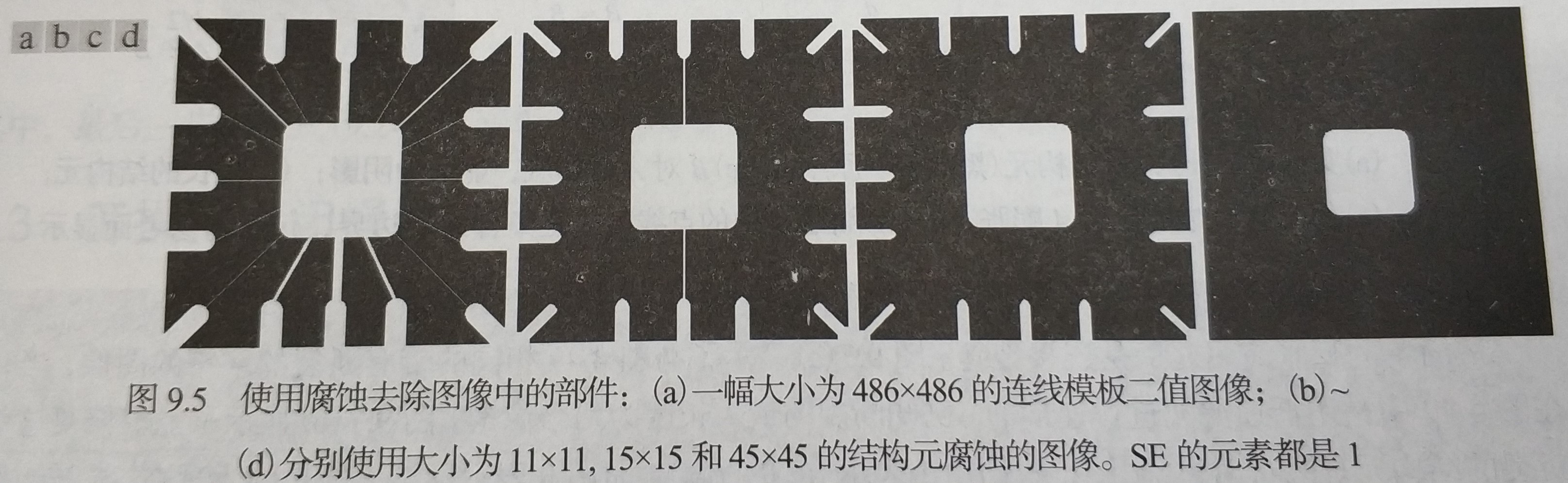 | 腐蚀缩小或细化了二值图像中的物体。事实上,我们可以将腐蚀视为形态学滤波操作,这种操作将小于结构元的图像细节从图像中滤除 |
 | 最简单的膨胀应用之一是连接裂缝。如左的形态学方法较之以前的低通滤波方法的一个直接优点是:形态学可在一幅二值图像中直接得到结果;而低通滤波方法从一幅二值图像先生成一幅灰度图像,然后通过阈值再回到二值图像 |
3. 开操作与闭操作
设一集合和结构元,对的开操作和闭操作分别写作和,有如下定义:
- 开操作:
- 闭操作:
开操作一般会平滑物体的轮廓、断开较窄的狭颈并消除较细的突出物;闭操作也会平滑轮廓的一部分,但通常会弥合较窄的间断和细长的沟壑、消除较小的孔洞、填补轮廓线中的断裂。
| 操作 | 几何解释 | 图示 |
|---|---|---|
| 开操作 | 1) 可把结构元 B 视为一个扁平的转球,的边界由 B 中的点建立:令 B 在 A 的边界内侧滚动,B 所能达到的 A 的边界的最远点 2) 注意:开操作使得方向向外的角变圆,而方向向内的角不变 | 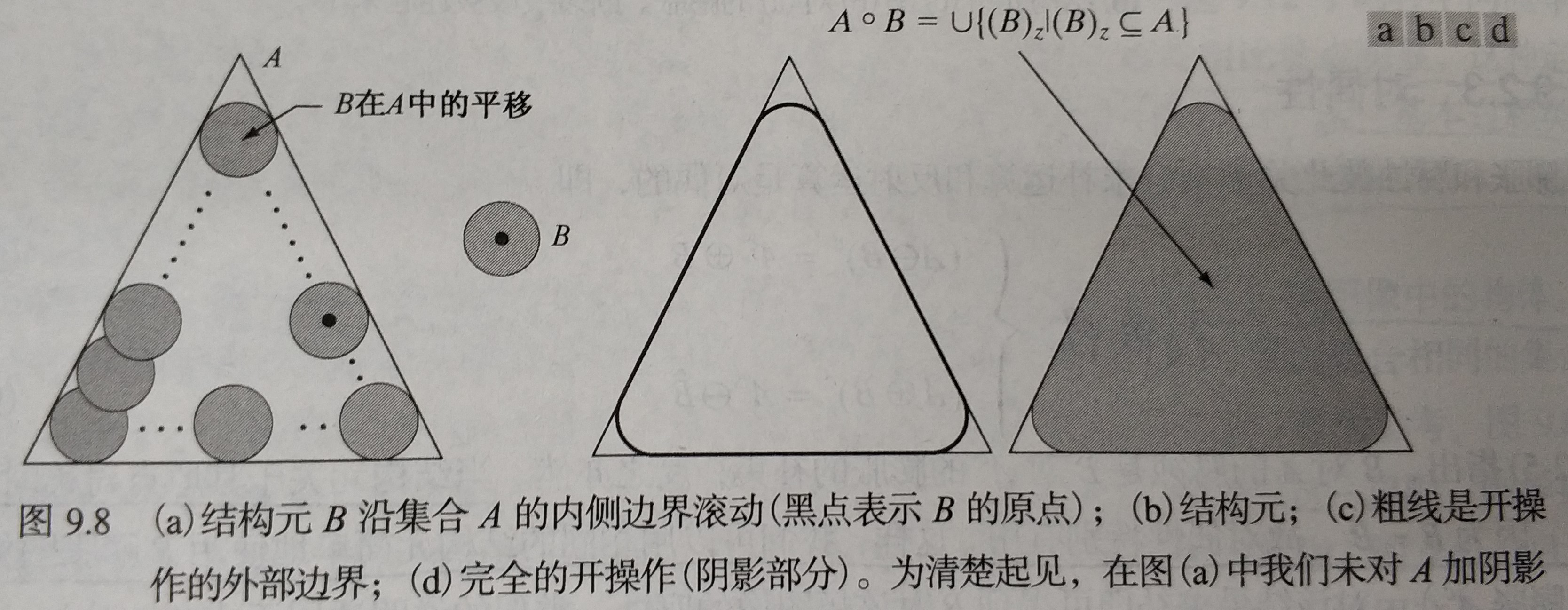 |
| 闭操作 | 1) 可把结构元 B 视为一个扁平的转球,的边界由 B 中的点建立:令 B 在 A 的边界外侧滚动,B 所能达到的 A 的边界的最远点。 2) 注意:闭操作使得方向向内的角变圆,而方向向外的角不变 | 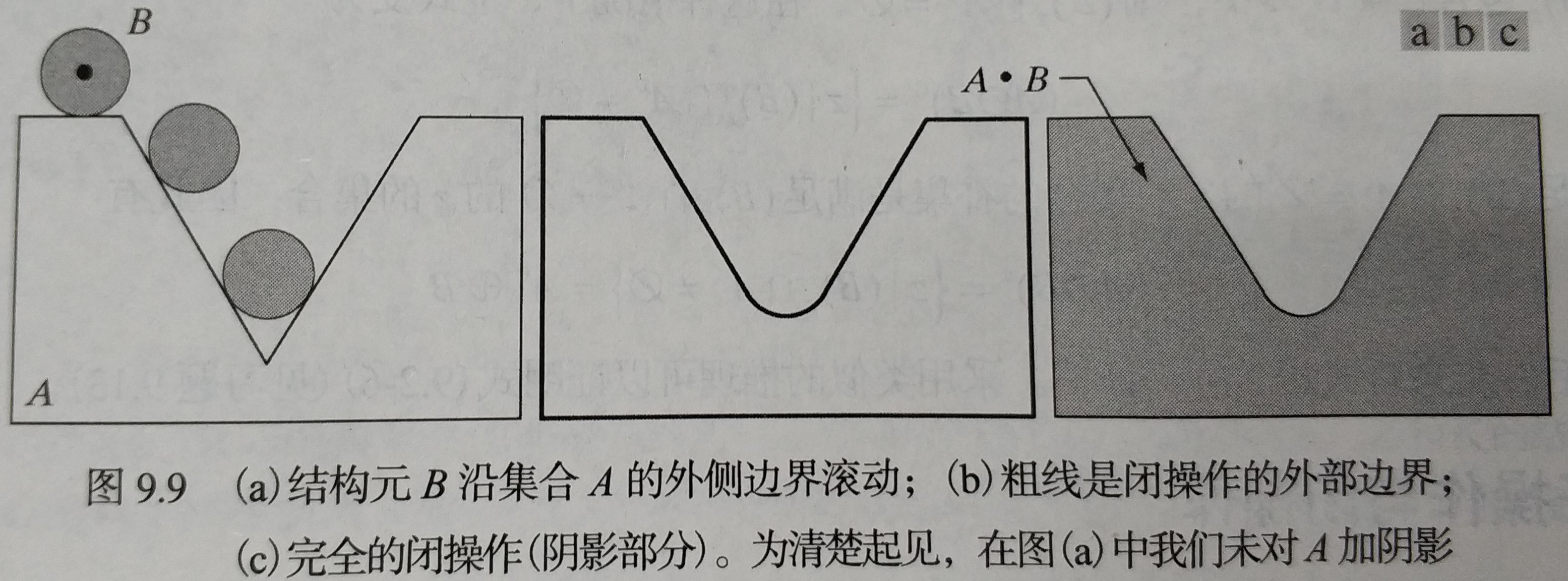 |
开/闭操作的性质:
开操作
- 是的一个子集
- 如果是的一个子集,则是的一个子集
闭操作
- 是的一个子集
- 如果是的一个子集,则是的一个子集
开-闭操作对偶性
开/闭操作也可以用于构建类似空间滤波概念的滤波器,如下:

4. 基本的形态学算法
4.1 边界提取
设有集合,为的边界,为一个适当的结构元,边界提取为:
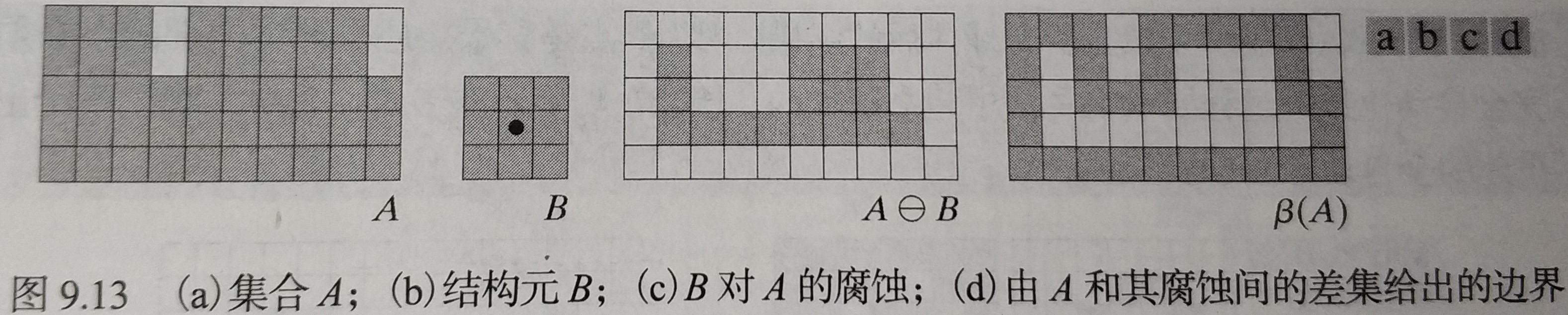 |
|---|
 |
4.2 孔洞填充
孔洞定义为由前景像素相连接的边界所包围的背景区域。令表示一个集合,为结构元,当给定每个孔洞中的一个点后,目的就是用 1(白色)填充所有的孔洞:
 |  |
|---|
4.3 连通分量提取
从二值图像中提取连通分量是许多自动图像分析应用的核心。令是包含一个或多个连通分量的集合,并形成一个阵列, 的大小与包含的阵列大小相同,是一个适当的结构元,其形状在像素间是基于 8 连通的,如下迭代可完成连通分量的提取:
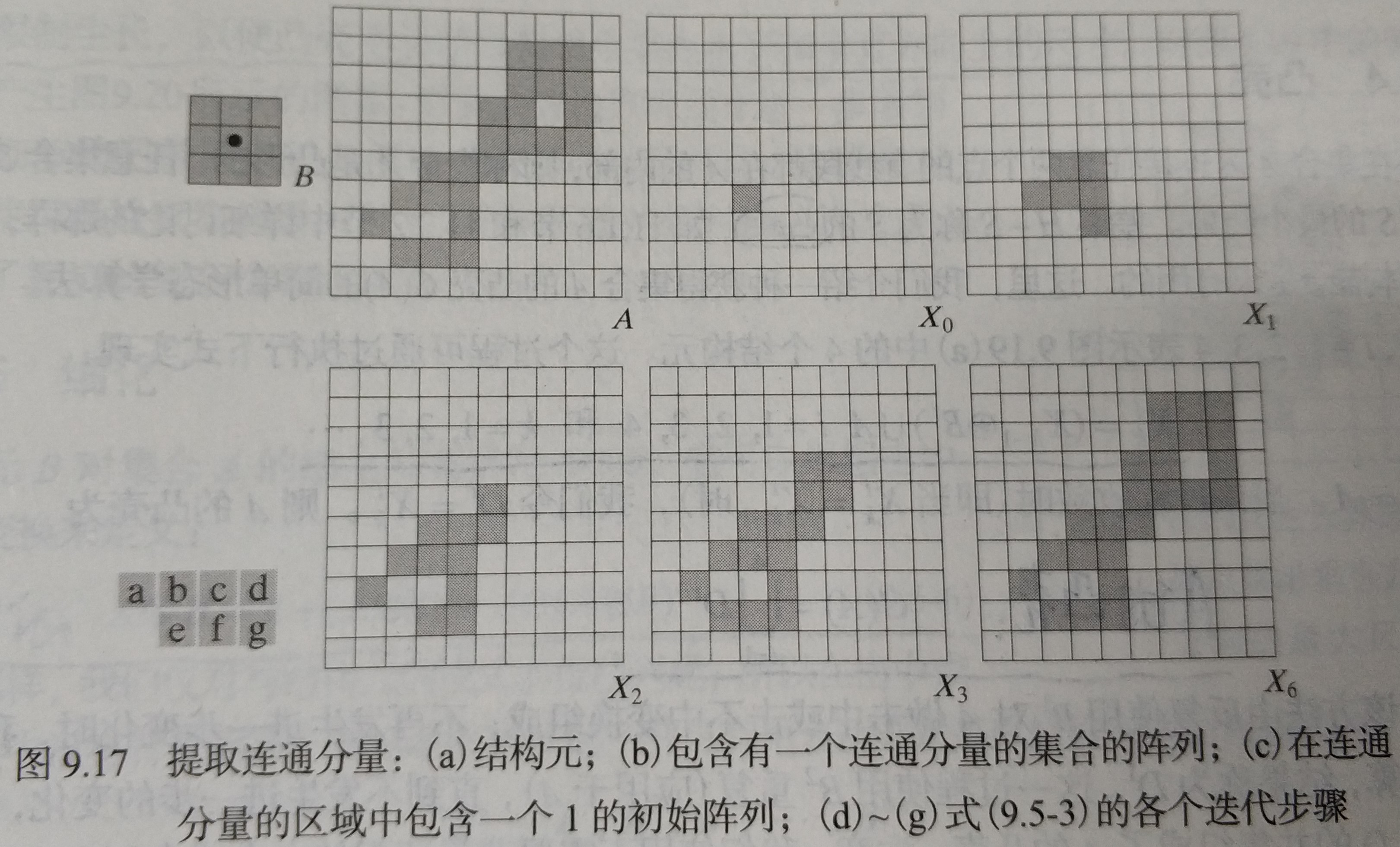 |
|---|
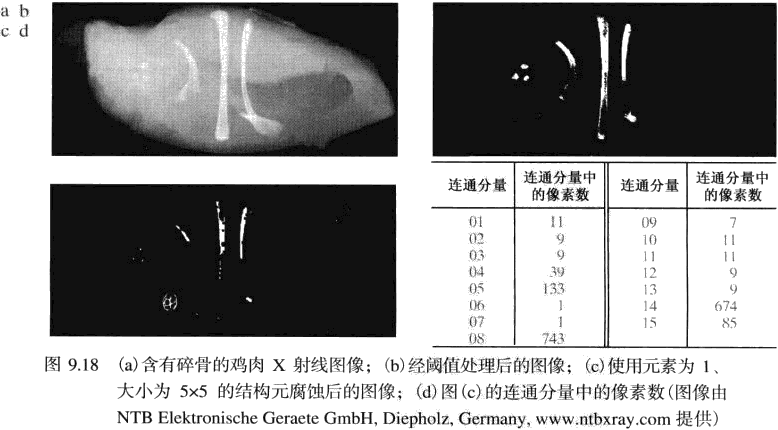 |
4.4 凸壳
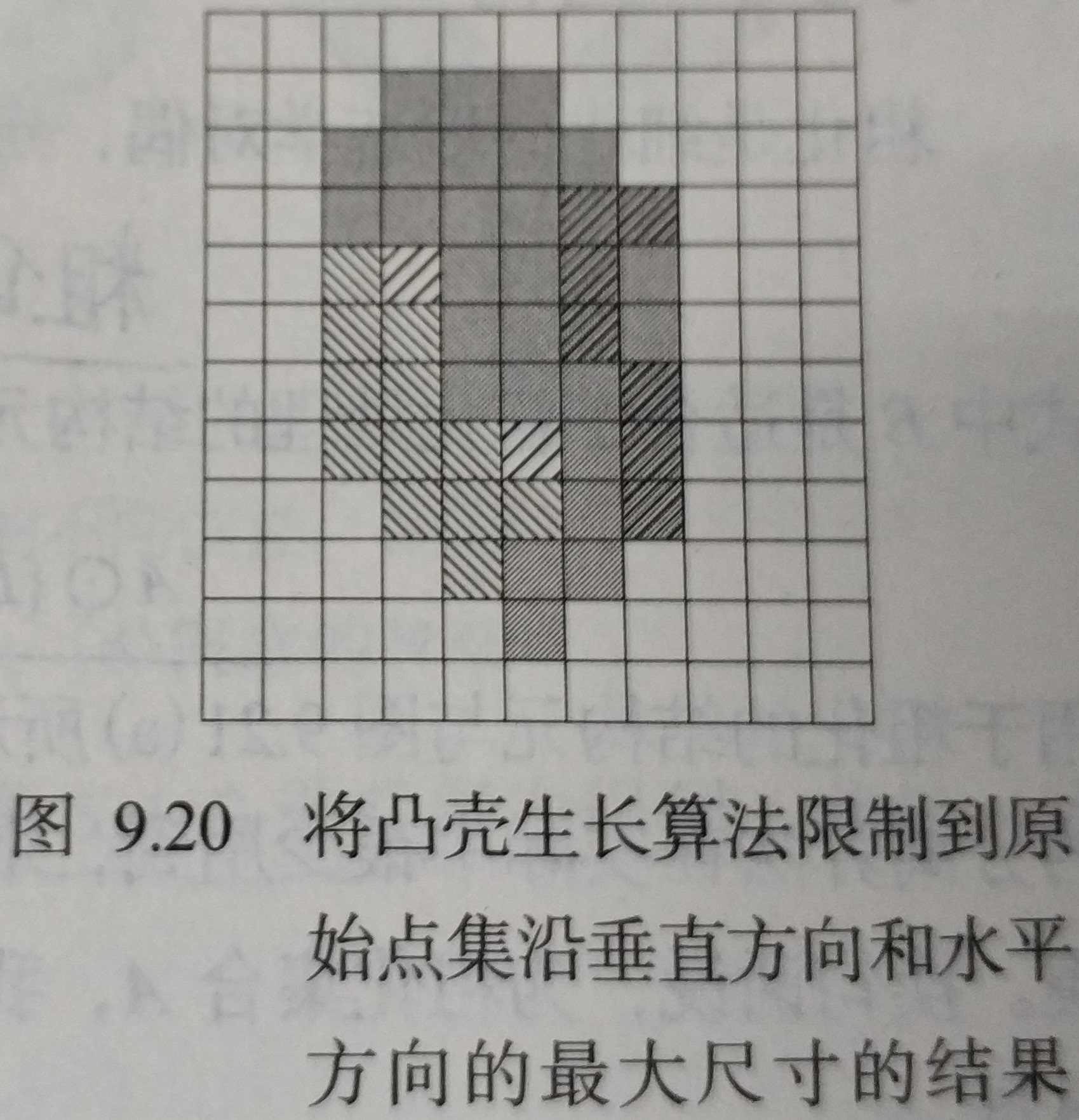
如果在集合内连接任意两个点的直线段都在的内部,则称集合是凸形的。任意集合的凸壳是包含于的最小凸集,差集称为的凸缺。的凸壳表示为,表示第个结构单元,下图的表示不考虑的条件。
其中表示击中或击不中变换,收敛时。
其中, 。
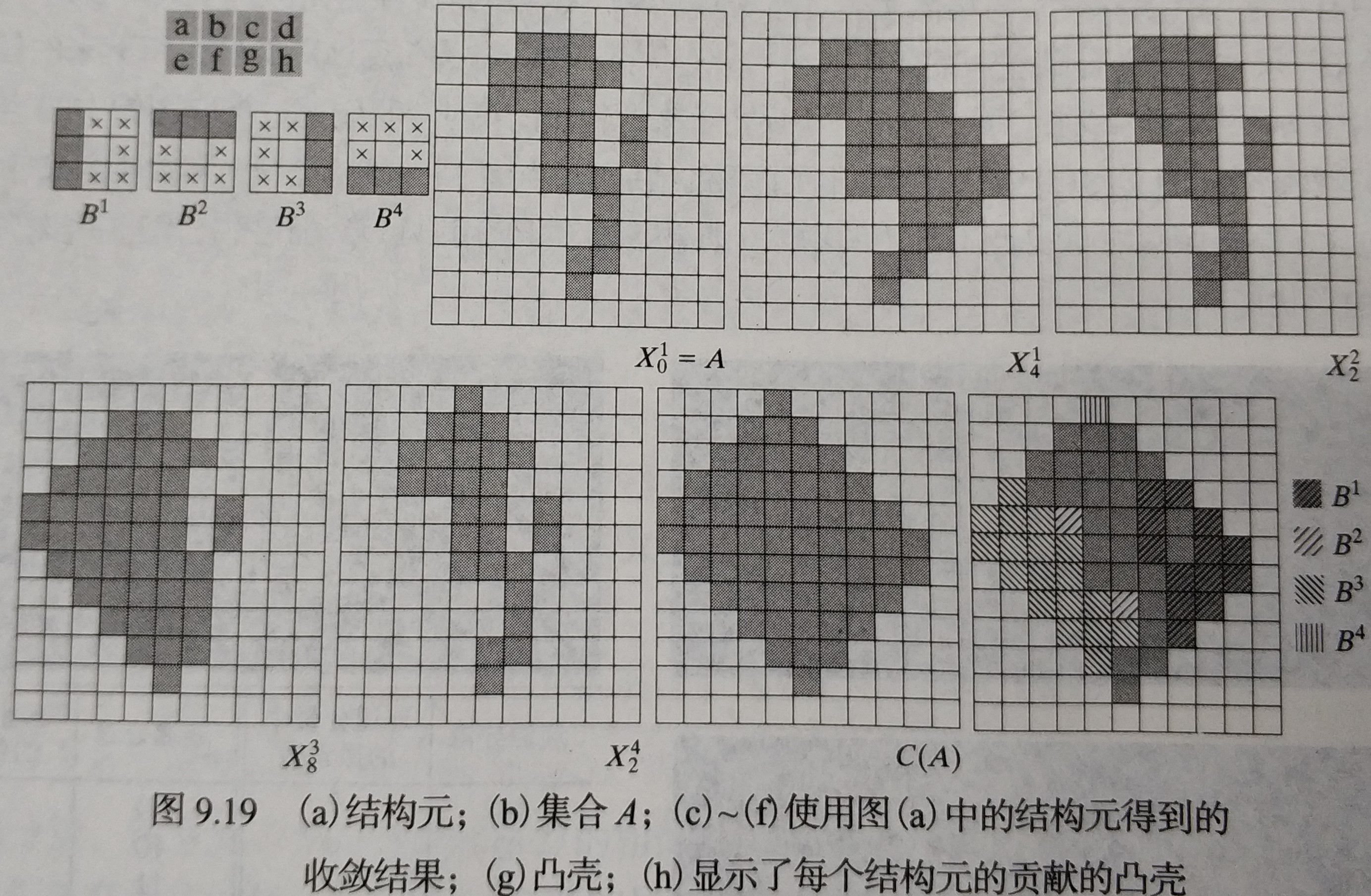 |  |
|---|
4.5 细化
结构元 B 对集合 A 的细化可表示为,其可根据击中击不中变换来定义:

4.6 粗化
粗化是细化的形态学对偶,用表示,以 A 为集合 B 为结构元,有如下定义(注意,由于依赖于 A 的性质,粗化过程可能会产生某些断点,如下图所示。故而,这种方法的粗化处理通常会跟随一个消除断点的后处理)。

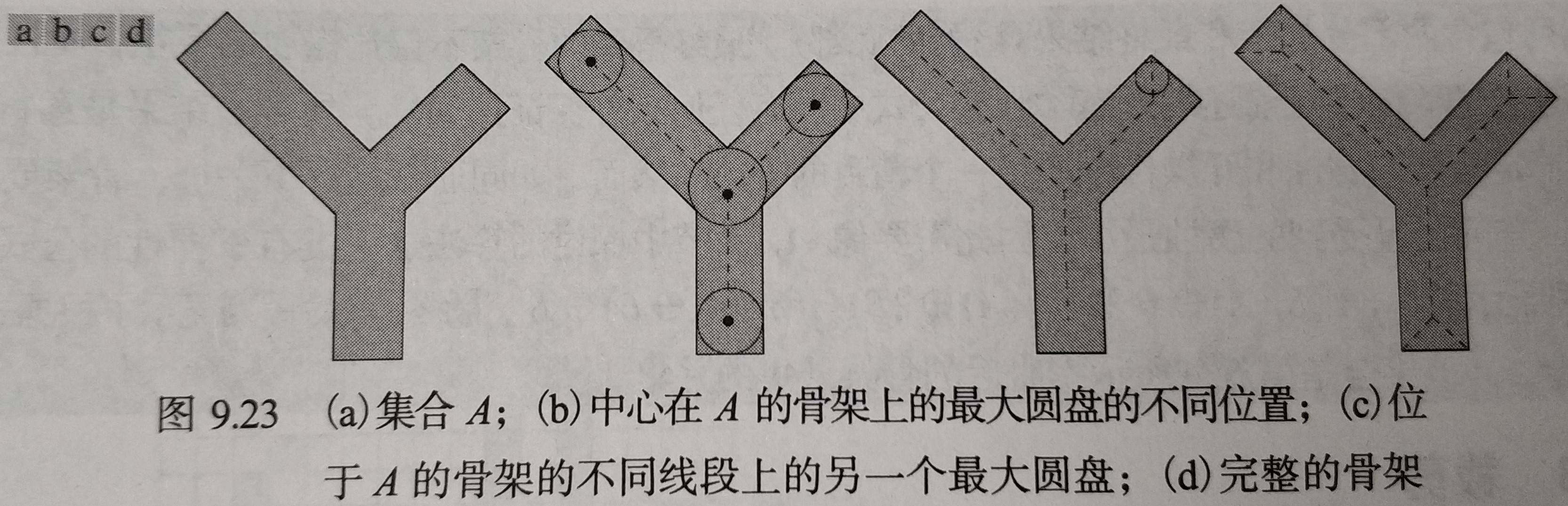
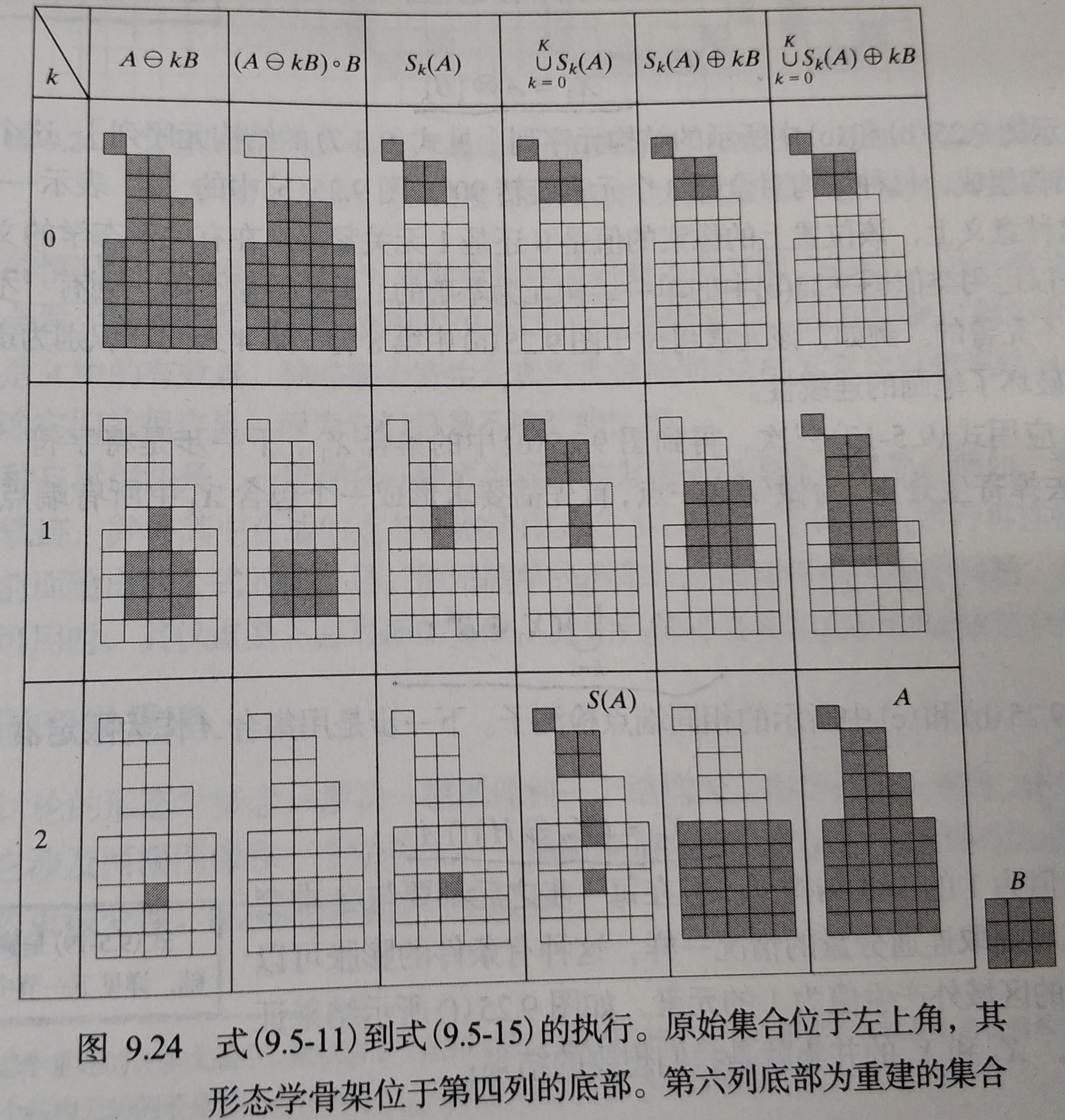
4.7 骨架
集合 A 的骨架为,如图所示,以 B 为一个结构元,有
 |
|---|
 |
4.8 裁剪
裁剪本质上是对细化和骨架算法的补充,因为这些过程会保留某些寄生成分,需要用后处理来消除这些寄生成分。以一个手写字母为例来说明裁剪过程:

4.9 形态学重建
不同以上,它涉及两幅图像和一个结构元:一幅图像是标记,包含变换的起始点;另一幅图像是模板,用来约束该变换;结构元则用来定义连接性。
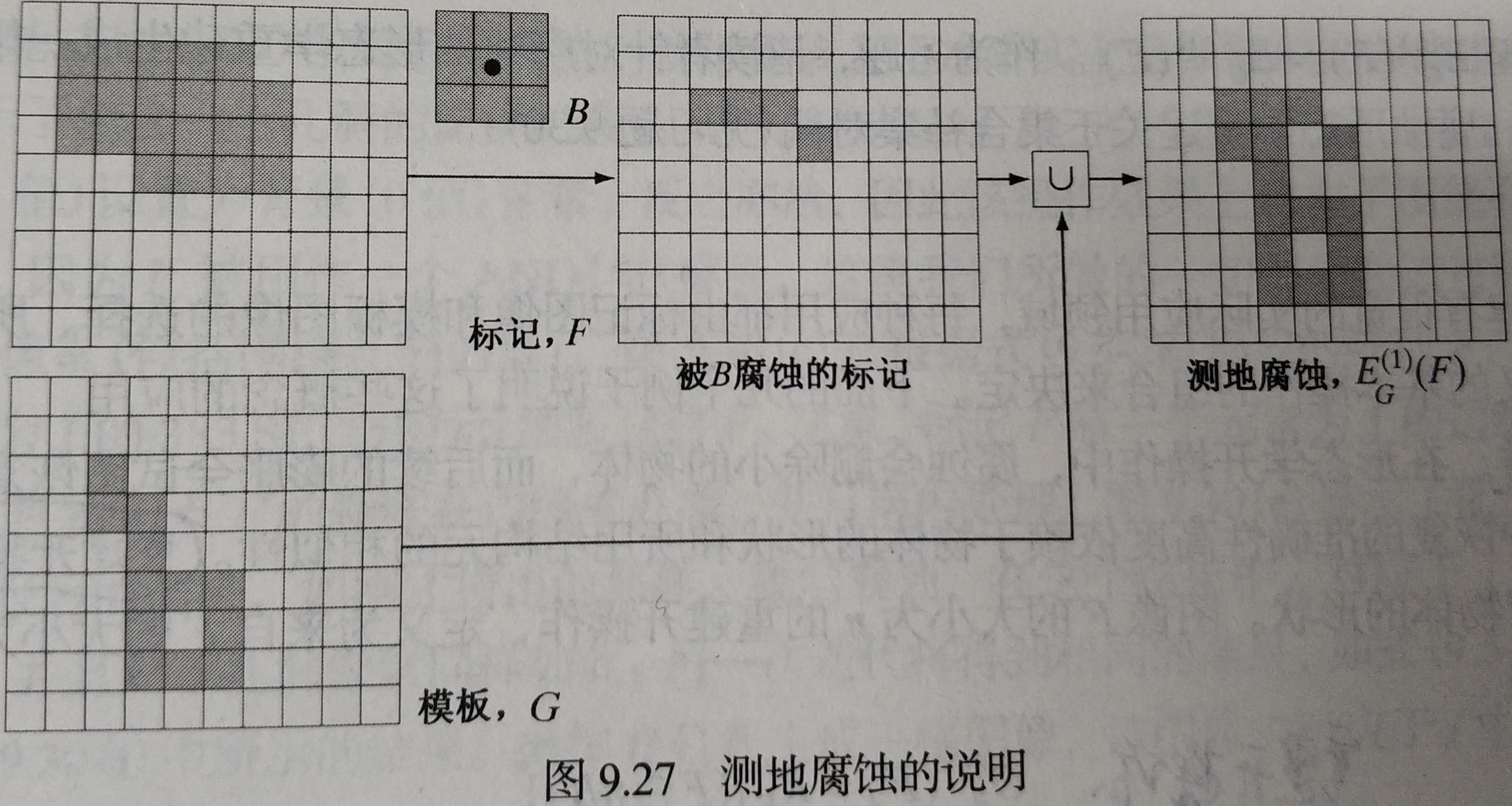
形态学重建的核心是测地膨胀和测地腐蚀两个概念,令表示标记图像,表示模板图像,两幅图像都是二值图像且。令表示大小为 1 的标记图像关于模板的测地膨胀,表示关于的大小为的测地膨胀,且;令表示关于的大小为 1 的测地腐蚀,表示关于的大小为的测地腐蚀,且。
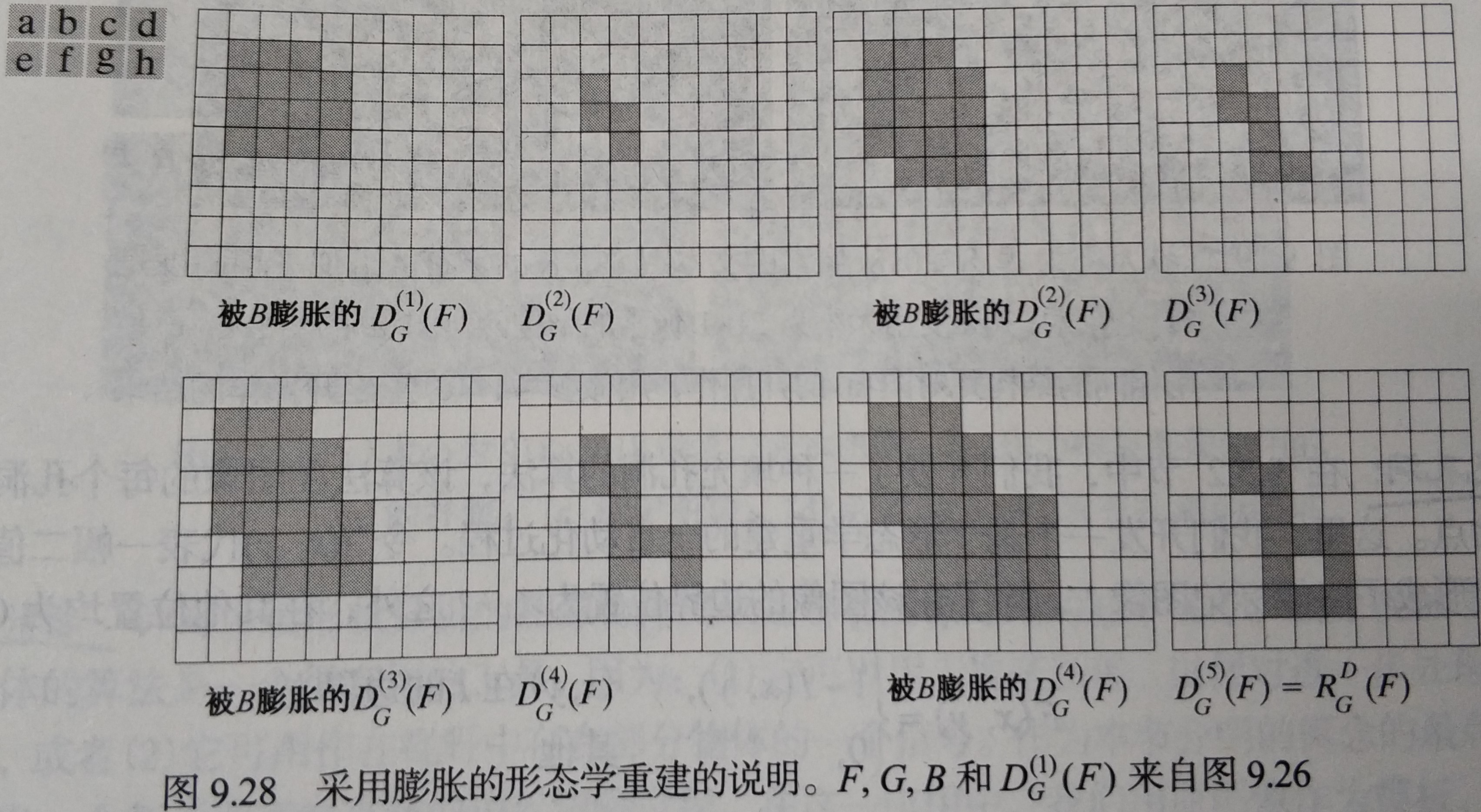
模板图像对标记图像的膨胀形态学重建表示为,它被定义为关于的测地膨胀,反复迭代次直至达到稳定状态,即。
模板图像对标记图像的腐蚀形态学重建表示为,它被定义为关于的测地腐蚀,反复迭代次直至达到稳定状态,即。
测地膨胀
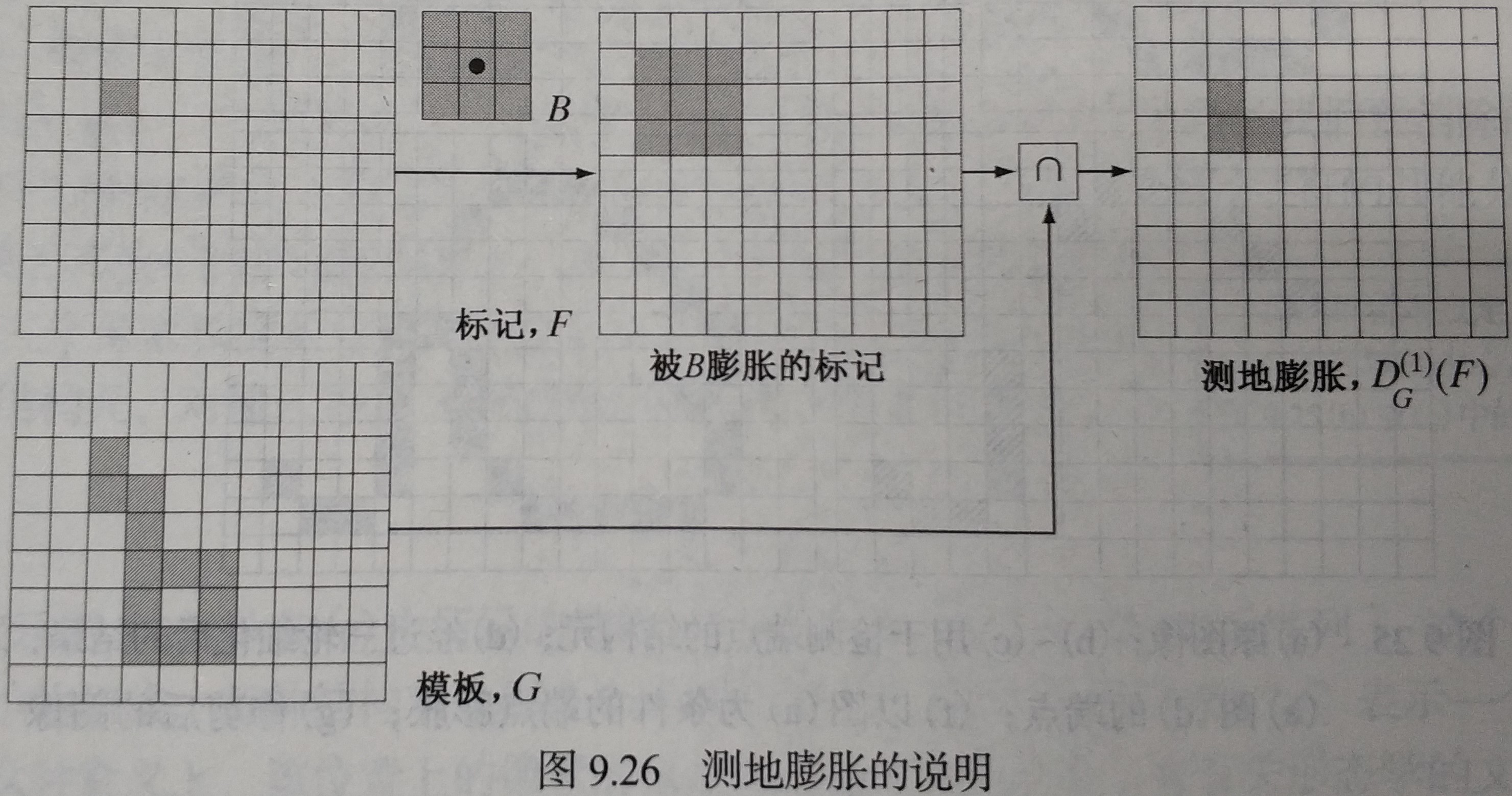
测地腐蚀
膨胀形态学重建
腐蚀形态学重建
5. 分水岭算法
形态学分水岭算法是一种图像分割算法。
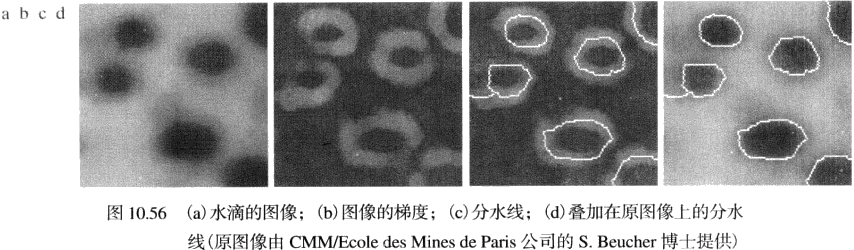
分水岭算法的主要应用之一是从背景中提取出灰度近乎一致的物体(类似于水滴)。
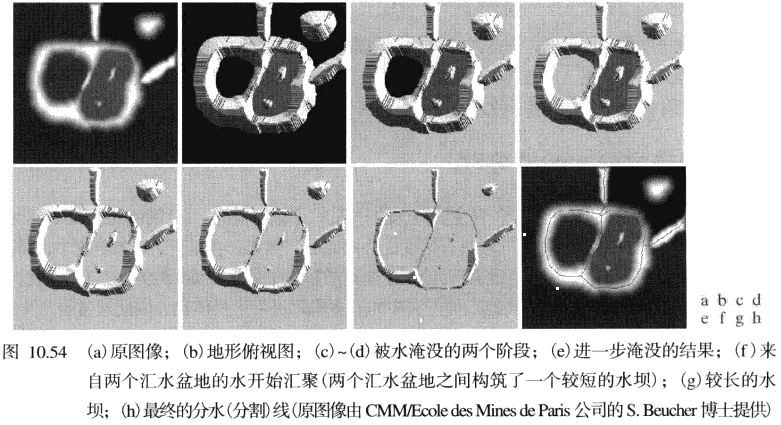
基本思想:对于一张灰度图像,假设在每个区域(“盆地”)的灰度最小值上打一个洞,并且让水通过洞以均匀的速率上升,水将从底到高渐渐淹没整个地形。所谓“地形”,其各点高度与对应像素的灰度值成正比,最高山峰的高度取决于输入图像灰度级中的最大值。当不同“汇水盆地”中上升的水即将没过彼此的边界而产生聚合时,修建一个“水坝”来阻止这种聚合。由此,试图淹没整张图片的水最终将形成一个只能显露出各个水坝顶部的水平面(当然,假设“水”不会从这张图像的边缘流出)。分水岭算法就以这些最后露出的坝顶为图像分割线,故而得名。
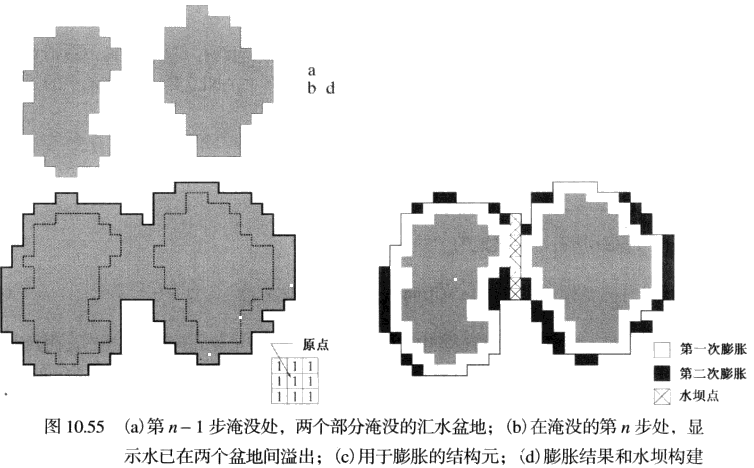
“水坝”的构建是以二值图像为基础的,其最简单的方法即是使用形态学膨胀。如下图:
分水岭算法的具体步骤不介绍,因为自己的工作主要是直接调包,详见 P.499 或其他文献。以下为另一分水岭算法的应用案例:
更新日志
899db-于eedbf-于baea0-于47fa5-于c9215-于9e065-于75141-于730b3-于de348-于dad0f-于7432d-于23b25-于c9318-于
