频率域滤波

1. 傅里叶变换和卷积

用傅里叶级数或变换表示的函数特征完全可以通过傅里叶反变换来重建，且不会丢失任何信息，这是这种表示方法的最重要特征之一。

1.1 傅里叶变换

傅里叶级数——具有周期$T$的连续变量$t$的周期函数$f(t)$可描述为乘以适当系数的正弦和余弦之和，这个和就是傅里叶级数。

傅里叶级数	欧拉公式
$f(t)=\sum_{n=-\infty}^{\infty} c_{n} e^{j \frac{2 \pi n}{T} t}, n=0, \pm 1, \pm 2, \ldots\\其中,c_{n}=\frac{1}{T} \int_{-T / 2}^{T / 2} f(t) e^{-j \frac{2 \pi n}{T} t} d t$	$e^{j \theta}=\cos \theta+j \sin \theta$

设连续变量 $t$ 和 $\mu$，有连续函数 $f(t)$ 的傅里叶变换对为

傅里叶变换	傅里叶反变换
$F(\mu)=\int_{−\infty}^{\infty}f(t)e^{−j2{\pi}{\mu}t}\mathrm{d}t$	$f(t)=\int_{−\infty}^{\infty}F(\mu)e^{j2{\pi}{\mu}t}\mathrm{d}\mu$

因为$f(t)$的傅里叶变换 $\mathfrak{\Im}\{f(t)\}=F(\mu)=\int_{-\infty}^{\infty} f(t) e^{-j 2 \pi \mu t} d t=\int_{-\infty}^{\infty} f(t)[\cos (2 \pi \mu t)-j \sin (2 \pi \mu t)] d t$ 积分后，左边剩下的唯一变量是频率$μ$，故称傅里叶变换域是频率域。其中，当变量$t$用于图像时，将变量$t$的域称为空间域。

1.2 卷积

两个函数的卷积相当于一个函数关于原点旋转 180° 然后滑过另一个函数，在滑动过程中的每一个位移处，执行相应计算。连续变量 $t$ 的两个连续函数 $f(t)$和 $h(t)$的卷积公式为：

$$f(t)⊛h(t)=\int_{−∞}^∞f(τ)h(t−τ)dτ \\ 其中，负号表示翻转180\degree，t是一个函数滑过另一个函数的位移，τ是积分假变量$$

卷积定理为：

$f(t)⊛h(t)⇔H(μ)F(μ)$	$f(t)h(t)⇔H(μ)⊛F(μ)$

1. 空间域中两个函数的卷积的傅里叶变换，等于两个函数的傅里叶变换在频率域中的乘积；换句话说，如果有两个傅里叶变换的乘积，那么可以通过计算傅里叶反变换得到空间域的卷积。即，$f(t)⊛h(t)$和$H(μ)F(μ)$是傅里叶变换对：$f(t)⊛h(t)⇔H(μ)F(μ)$
2. 频率域的卷积类似于空间域的乘积，两者分别与傅里叶正、反变换相联系。即， $f(t)h(t)⇔H(μ)⊛F(μ)$ 卷积定理是频率域滤波的基础。

2. 冲激与取样

用计算机处理前连续函数必须转换为离散序列，故就需要利用冲激来进行取样量化。

2.1 冲激及其取样特性

冲激及其取样特性（线性变换和傅里叶变换的核心）：

• 对于连续变量$t$

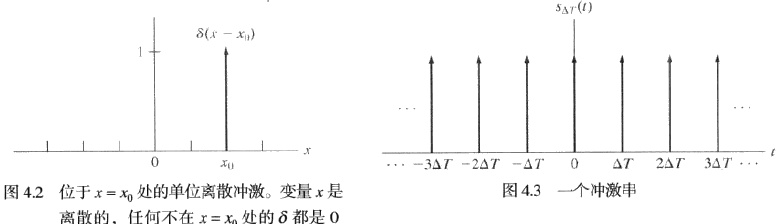
  • 连续变量$t$在$t=0$处的单位冲激表示为$δ(t)$

    $$\delta(t)=\left\{\begin{array}{ll}\infty, & t=0 \\ 0, & t \neq 0\end{array}\right. \\ \\ \int_{-\infty}^{\infty} \delta(t) d t=1$$

    物理上，如果我们把$t$解释为时间，那么一个冲激可视为幅度无限、持续时间为 0、具有单位面积的尖峰信号

  • 连续变量的冲激具有如下取样特性

    • 取样特性：$\sum_{x=-\infty}^{\infty} f(x) \delta(x)=f(0)$
    • 一般化的取决特性：$\sum_{x=-\infty}^{\infty} f(x) \delta\left(x-x_{0}\right)=f\left(x_{0}\right)$

• 对于离散变量$x$

  

  • 单位离散冲激$δ(x)$在离散系统中的作用与连续变量相同

    $\delta(x)=\left\{\begin{array}{ll}1, & x=0 \\ 0, & x \neq 0\end{array}\right.$	$\sum_{-\infty}^{\infty}\delta(x)=1$

  • 离散变量的取样特性

    取样特性	一般化地用位置$x=x_0$处的离散冲激
    $\sum_{x=-\infty}^{\infty} f(x) \delta\left(x\right)=f\left(0\right)$	$\sum_{x=-\infty}^{\infty} f(x) \delta\left(x-x_{0}\right)=f\left(x_{0}\right)$

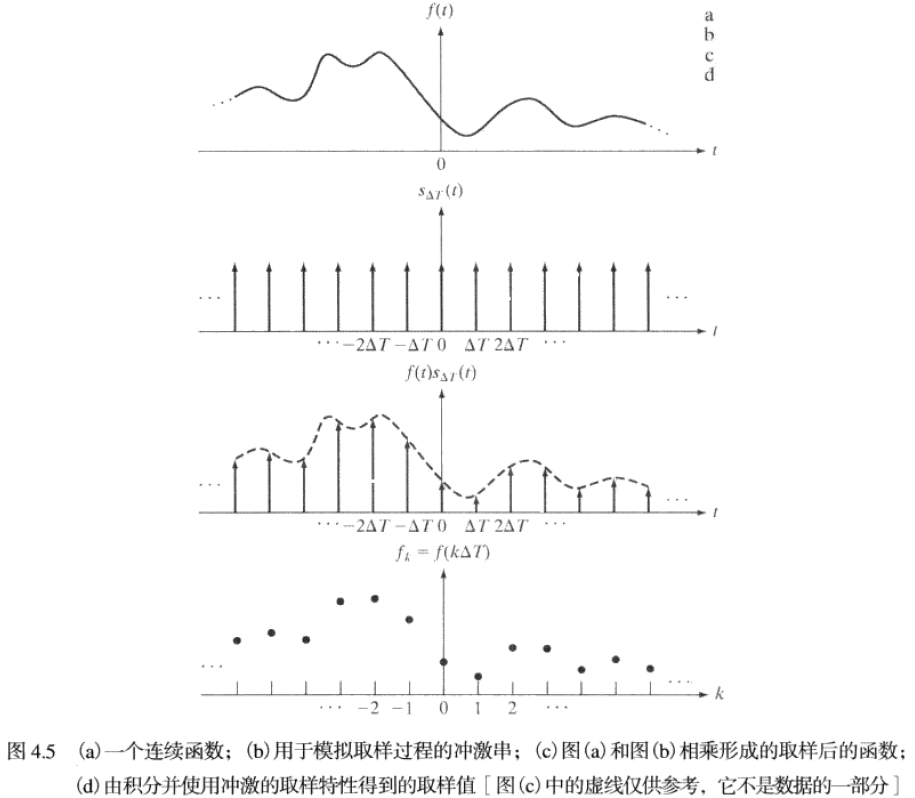
  • 冲激串$s_{\Delta T}(t)$：定义为无限多个离散的周期冲激单元$ΔT$之和

    $$s_{\Delta T}(t)=\sum_{n=-\infty}^{\infty} \delta(t-n \Delta T)$$

---

对一个连续函数$f(t)$，假设函数关于$t$从$−∞$扩展到$∞$，我们希望以自变量$t$的均匀间隔$ΔT$来取样。可利用一个$ΔT$单位间隔的冲激串作为取样函数去乘以$f(t)$，得取样后的函数$\tilde{f}(t)$，即

$$\tilde{f}(t)=f(t) s_{\Delta T}(t)=\sum_{n=-\infty}^{\infty} f(t) \delta(t-n \Delta T)=f(n \Delta T), \quad n \in \mathbb{Z}$$

和式中每一分量都是该冲激位置处$f(t)$的值加权后的冲激，即每个取样值由加权后的冲激强度给出。

取样函数$\tilde{f}(t)$的傅里叶变换$\mathfrak{\Im}\{f(t)\}$为：

$$\tilde{F}(\mu)=\mathfrak{\Im}\{\tilde{f}(t)\}=\mathfrak{\Im}\left\{f(t) s_{\Delta T}(t)\right\}=F(\mu) \circledast S(\mu)=\frac{1}{\Delta T} \sum_{n=-\infty}^{\infty} F\left(\mu-\frac{n}{\Delta T}\right)$$

上式表明，傅里叶变换$\tilde{F}(\mu)$是$F(μ)$的一个副本的无限、周期序列，也是原始连续函数的傅里叶变换。副本间的间隔由$\frac{1}{ΔT}$ 的值决定。虽然$\tilde{f}(t)$是取样后的函数，但其变换$\tilde{F}(\mu)$是连续的，因为它由$F(μ)$的若干副本组成。

2.2 取样定理

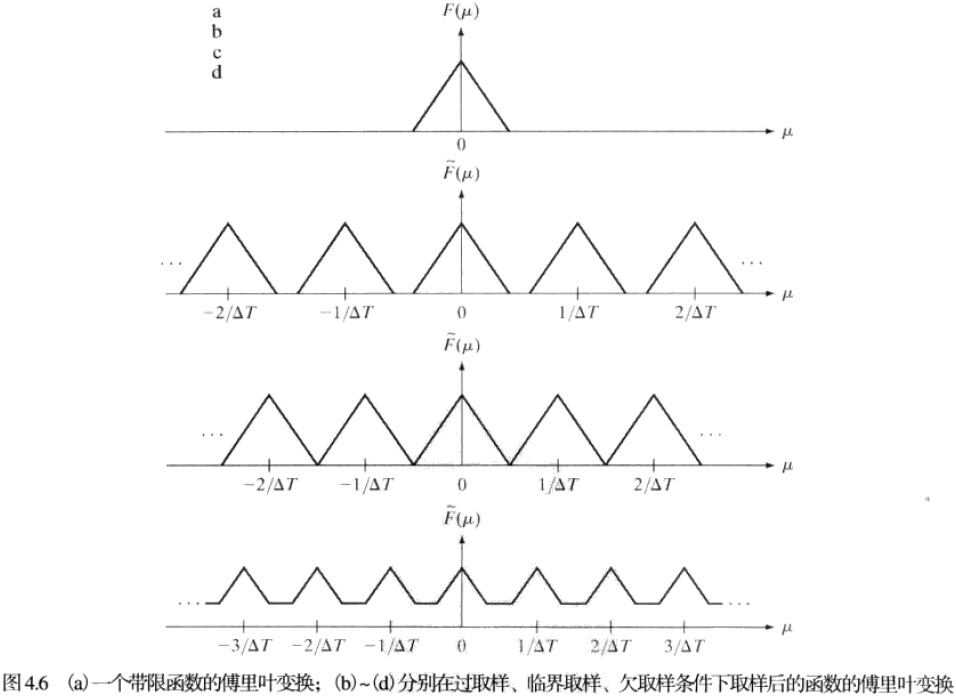
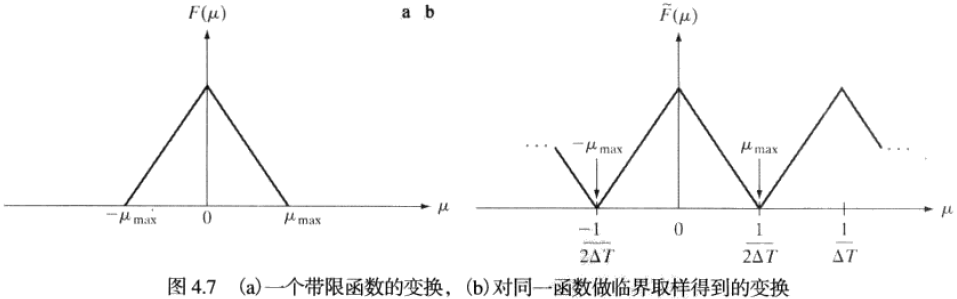
设某函数$f(t)$与其傅里叶变换$F(μ)$，若$F(μ)$在以原点为中心的有限区间（带宽）$[−μ_{max},μ_{max} ]$之外均为零，则称函数$f(t)$为带限函数。

对于一个连续带限函数$f(t)$，若取样率大于$2μ_{max}$，在$f(t)$能完全由其样本集进行恢复，这就是所谓的取样定理。其中$2μ_{max}$ 称为奈奎斯特取样率。

基于取样定理，若一个连续带限函数用取样率大于函数最高频率两倍的取样来表示，则不会有信息损失；反之，以 $\frac{1}{ΔT}$ 的取样率对一个信号取样的最大频率是$\mu_{max}=\frac{1}{2ΔT}$ 。

2.3 频率混淆

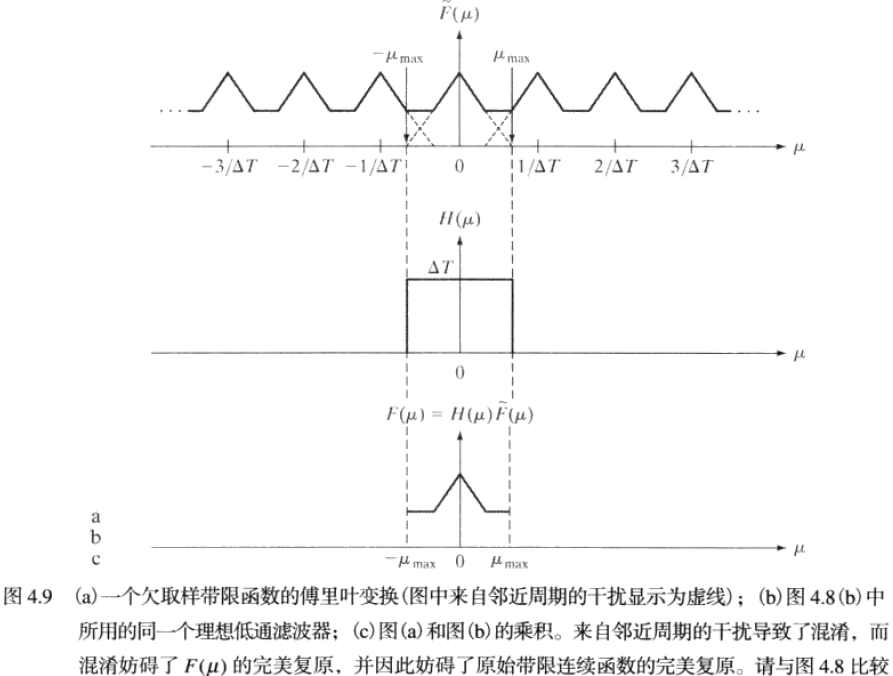
如果以低于奈奎斯特取样率取样，会产生周期重叠，且不管使用什么滤波器都无法分隔出变换的单个周期。

由函数欠取样导致的频率破坏就是频率混淆，简称为混淆。混淆是一个过程，在这一过程中，连续函数的高频成分在取样后的函数中被低频“化妆”了。

遗憾的是，除了某些特殊情况，在取样后的函数中混淆总是存在的。

3. 离散傅里叶变换和卷积

3.1 离散傅里叶变换对

离散傅里叶变换（Discrete Fourier Transformation, DFT）与离散傅里叶反变换（Inverse DFT, IDFT）。

如果$f(x)$由函数$f(t)$以$ΔT$为单位间隔取样后的$M$个样本组成，对于集合${f(x)|x=0,1,…,M−1}$，有其：

• 取样的持续时间：$T=MΔT$
• 频率分辨率（间隔）：$\Delta\mu=\frac{1}{M\Delta}=\frac{1}{T}$
• 跨越的频率范围：$\Omega=M\Delta\mu=\frac{1}{\Delta T}$

设有一个由连续函数$f(t)$的$M$个样本组成的集合$\{f_n\}$或${f(x)|x=0,1,…,M−1}$，其对应的$M$个离散傅里叶变换的值的样本集合为$\{F_m\}$或${F(μ)|μ=0,1,…,M−1}$。离散傅里叶变换对适用于任何均匀取样的有限离散样本集。

• DFT

  $$F_m=\sum_{n=0}^{M-1}{f_ne^{-j2\pi mn/M}}, \quad m=0,1,2,\cdots,M-1$$

  $$F(\mu)=\sum_{x=0}^{M-1}{f(x)e^{-j2\pi \mu x/M}}, \quad \mu=0,1,2,\cdots,M-1$$

• IDFT：

  $$f_{n}=\frac{1}{M} \sum_{m=0}^{M-1} F_{m} \mathrm{e}^{j 2 \pi m n / M}, \quad n=0,1,2, \cdots, M-1$$

  $$f(x)=\frac{1}{M} \sum_{\mu=0}^{M-1} F(\mu) \mathrm{e}^{j 2 \pi \mu x / M}, \quad x=0,1,2, \cdots, M-1$$

离散卷积公式：由于函数是周期的，所以它们的卷积也是周期的，下式也给出了周期卷积的一个周期。

$$f(x) \circledast h(x)=\sum_{m=0}^{M-1} f(m) h(x-m), \quad x=0,1,2, \ldots, M-1$$

3.2 二维拓展

在一维时，我们使用$t$和$x$分别表示连续和离散的空间变量，而为了突出频率域的主题，频率变量的连续和离散形式均用$μ$表示；扩展到二维情况，我们用$(t,z)$和$(x,y)$分别表示连续和离散的空间变量，用$(μ, ν)$同时表示连续的和离散的频率域变量。

二维傅里叶变换对

• 连续情况

  $$F(\mu, v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)e^{-j2\pi(\mu t+vz)}dtdz$$

  $$f(t,z)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(\mu,v)e^{j2\pi(\mu t+\nu z)}d\mu dv$$

• 离散情况

  $$F(\mu, v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(\mu x/M + vy/N)}$$

  $$f(x,y)=\frac{1}{MN}\sum_{\mu=0}^{M-1}\sum_{v=0}^{N-1}F(\mu, v)e^{j2\pi(\mu x/M+vy/N)}$$

二维冲激及其取样特性

• 连续变量

  • 冲激

    $$\delta(t,z)=\left\{\begin{array}{ll}\infty, & t=z=0 \\ 0, & 其他 \end{array}\right.$$

    $$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(t,z)dtdz=1$$

  • 取样特性

    $$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)\delta(t,z)dtdz=f(0,0)$$

    $$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)\delta(t-t_0, z-z_0)dtdz=f(t_0,z_0)$$

• 离散变量

  • 冲激

    $$\delta(x,y)=\left\{\begin{array}{ll}1, & x=y=0 \\ 0, & 其他 \end{array}\right.$$

  • 取样特性

    $$\sum_{x=-\infty}^{\infty} \sum_{y=-\infty}^{\infty} f(x, y) \delta(x, y)=f(0,0)$$

    $$\sum_{x=-\infty}^{\infty} \sum_{y=-\infty}^{\infty} f(x, y) \delta\left(x-x_{0}, y-y_{0}\right)=f\left(x_{0}, y_{0}\right)$$

二维取样定理：

• 对于函数$f(t,z)$，若其在由区间$[−μ_{max},μ_{max} ]$和$[−v_{max},V_{max} ]$构成的矩形之外的傅里叶变换值均为零，则称函数$f(t,z)$为二维的带限函数，即

  $$F(\mu, v)=\mathfrak{\Im}\{f(t, z)\}=0, \quad|\mu| \geqslant \mu_{\max } \;且\; |v| \geqslant v_{\max }$$

• 二维取样定理：对于一个二维带限连续函数$f(t,z)$，若其表示样本的取样频率在$μ$和$v$两个方向上均大于该函数最高频率的两倍，则没有信息丢失。

图像中的混淆

在图像中存在两种主要的混淆，空间混淆和时间混淆，这里主要关注空间混淆。

空间混淆由欠取样导致，如线状特征中的锯齿、伪高光、原图像中不存在的模式等。

时间混淆与图像序列中图像间的时间间隔有关，最常见的例子是“车轮效应”，即在序列图像（如电影）中具有轮福的车轮出现倒转的现象，这是由序列中的帧率低于车轮速度引起的。

一幅数字图像缩小后，混淆效应通常会变得更严重。

当我们处理具有很强的边缘内容的图像时，混淆的影响看起来就像是块状图像成分，称为锯齿。

3.3 二维 DFT 的性质

假设对连续函数$f(t,z)$取样生成了一幅数字图像$f(x,y)$，它由分别在$t$和$z$方向所取的$M×N$个样本点组成，令$\Delta T$和$\Delta Z$分别表示样本间的间隔，相应离散频率域变量间的间隔分别为$\Delta μ$和$\Delta v$，有如下特性：

• 频率间隔与空间间隔的关系

  $$\Delta \mu=\frac{1}{M\Delta T}$$

  $$\Delta v=\frac{1}{N\Delta Z}$$

• DFT 变换对的平移特性（平移不影响$F(μ,v)$的幅度）

  $$f(x, y) \mathrm{e}^{j 2 \pi\left(\mu_{0} x / M+v_{0} y / N\right)} \Leftrightarrow F\left(\mu-\mu_{0}, v-v_{0}\right)$$

  $$f\left(x-x_{0}, y-y_{0}\right) \Leftrightarrow F(\mu, v) \mathrm{e}^{-j 2 \pi\left(x_{0} \mu / M+y_{0} v / N\right)}$$

• DFT 变换对的旋转特性（$f(x,y)$与$F(μ,v)$的总是保持同步的旋转角度）

  $$f\left(r, \theta+\theta_{0}\right) \Leftrightarrow F\left(\omega, \varphi+\varphi_{0}\right)$$

  $$x=r \cos \theta, \quad y=r \sin \theta, \quad \mu=\omega \cos \varphi, \quad v=\omega \sin \varphi$$

• DFT 与 IDFT 的周期性（其中$k_1$和$k_2$是整数）

  $$F(\mu, v)=F\left(\mu+k_{1} M, v\right)=F\left(\mu, v+k_{2} N\right)=F\left(\mu+k_{1} M, v+k_{2} N\right)$$

  $$f(x, y)=f\left(x+k_{1} M, y\right)=f\left(x, y+k_{2} N\right)=f\left(x+k_{1} M, y+k_{2} N\right)$$

二维卷积定理，设$x=0,1,2,\cdots,M−1,\quad y=0,1,2,\cdots,N−1$，有：

• 二维（循环）卷积公式

  $$f(x,y)\circledast h(x,y)=\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)h(x-m,y-n)$$

• 二维卷积定理

  $$f(x,y)\circledast h(x,y) \Leftrightarrow F(\mu,v)H(\mu,v)$$

  $$f(x,y)h(x,y)\Leftrightarrow F(\mu,v) \circledast H(\mu,v)$$

令$R(μ,v)$和$I(μ,v)$分别为$F(μ,v)$的实部和虚部，$μ=0,1,2,\cdots,M−1,\; v=0,1,\cdots,N−1$，有如下二维 DFT 的傅里叶谱和相角等定义：（以下表明$|F(μ,v)|$，$\phi(\mu,v)$和$P(\mu,v)$是大小为$M×N$的阵列）

• DFT 的极坐标形式

  $$F(\mu,v)=|F(\mu,v)|e^{j\phi(\mu,v)}$$

• 傅里叶谱/频谱/DFT 的幅度

  $$|F(\mu,v)|=[R^2(\mu,v)+I^2(\mu,v)]^{1/2}$$

• 相角

  $$\phi(\mu,v)=\arctan[\frac{I(\mu,v)}{R(\mu,v)}]$$

• 功率谱

  $$P(\mu,v)=|F(\mu,v)|^2=R^2(\mu,v)+I^2(\mu,v)$$

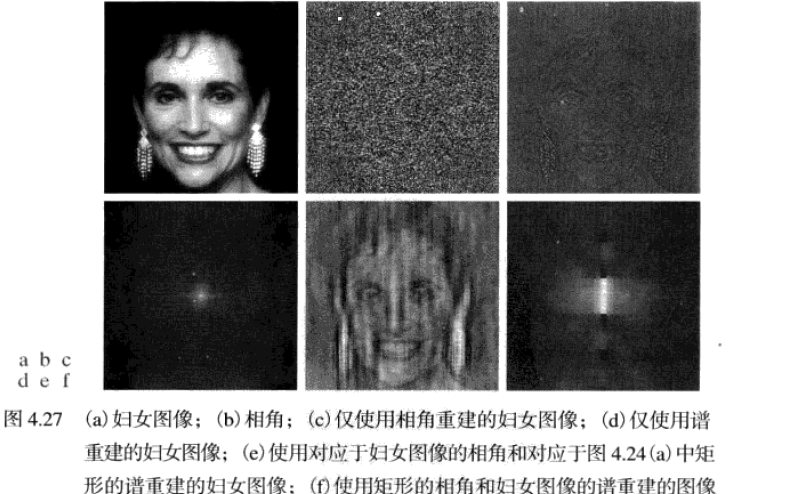
在一幅图像的 DFT 中，在任何给定的频率处，较大的幅度意味着图像中该频率的正弦波比较突出；反之，较小的幅度意味着图像中正弦波较少。虽然相角成分的贡献很不直观，但它非常重要，相角是各个正弦成分关于原点的位移的度量。这样，当二维 DFT 的幅度是一个阵列时，其成分就决定了图像中的灰度，相应的相角则是一个角度阵列，它携带较多关于图像中可辨别物体定位的信息。

4. 频率域滤波

4.1 概念

频率域滤波是指通过修改一幅图像的傅里叶变换，然后计算其反变换，得到处理后的结果。由此，给定一幅$M×N$的图像$f(x,y)$，其频率域滤波公式的基本形式为（其中，函数$F,H,g$是大小与$f(x,y)$相同的$M×N$阵列）：

$$g(x, y)=\mathfrak{\Im}^{-1}[H(\mu, v) F(\mu, v)]$$

$\mathfrak{\Im}^{-1}$是 IDFT，$F(\mu,v)$是输入图像$f(x,y)$的 DFT，$H(\mu,v)$是滤波器/滤波函数，$g(x,y)$是滤波后的输出图像。

空间滤波器$h(x,y)$和频率滤波器$H(μ,v)$构成了傅里叶变换对$h(x,y) \Leftrightarrow H(\mu,v)$，因为$h(x,y)$可以由$H(\mu,v)$对一个冲激的响应得到，故$h(x,y)$有时称为$H(\mu,v)$的脉冲响应。

频率域可被视为一个“实验室”，有些在空间域异常困难的或不可能直接用公式表达的任务，在频率域却变得很容易，因为经常在频率域中“操作实验”。

频率直接关系到空间变化率，傅里叶变换中的频率与图像中的亮度变化模式有直接关系。变换中的低频对应于图像中变化缓慢的灰度成分，如室内的墙壁和室外少云的天空；高频由灰度的尖锐过渡造成，如边缘和噪声等。

滤波器	定义	作用
低通滤波器	衰减高频而通过低频的滤波器	将模糊一幅图像
高通滤波器	衰减低频而通过高频的滤波器	将增强尖锐的细节，但降低图像对比度

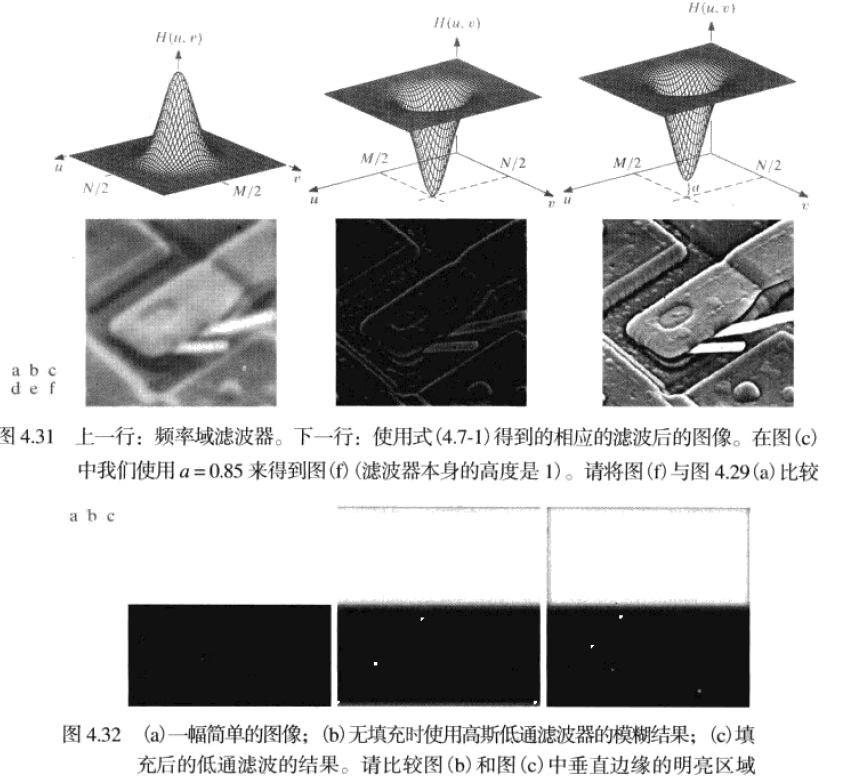
基于高斯函数的滤波器特别重要，因为一个高斯函数的正、反傅里叶变换都是实高斯函数。

使用频率域滤波器可平滑图像和锐化图像，分别依赖低通和高通滤波器。

4.2 步骤

1. 给定一幅大小为$M×N$的输入图像$f(x,y)$，根据$P≥2M−1$和$Q≥2N−1$选择填充参数$P$和$Q$，通常令$P=2M$和$Q=2N$；
2. 对$f(x,y)$添加必要数量的 0，形成大小为$P×Q$的填充图像$f_p (x,y)$。
3. 用$(−1)^{(x+y)}$ 乘以$f_p (x,y)$，移动其变换的中心；
4. 计算来自步骤 3 的图像的 DFT，得到$F(μ,v)$；
5. 生成一个实的、对称的滤波函数$H(μ,v)$，其大小为$P×Q$，中心在$(P/2,Q/2)$处。用阵列相乘形成乘积$G(μ,v)=H(μ,v)F(μ,v)$；
6. 得到处理后的图像$g_p(x, y)=\{real[\mathfrak{\Im}^{-1}[G(\mu,v)]]\}(-1)^{x+y}$，其中，为忽略由于计算不准确导致的寄生复成分，选择了实部，下标注$p$指出我们处理的是填充后的阵列；
7. 从$g_p (x,y)$的左上象限提取$M×N$区域，得到最终处理结果$g(x,y)$。

4.3 低通滤波器

理想低通滤波器（ILPF）

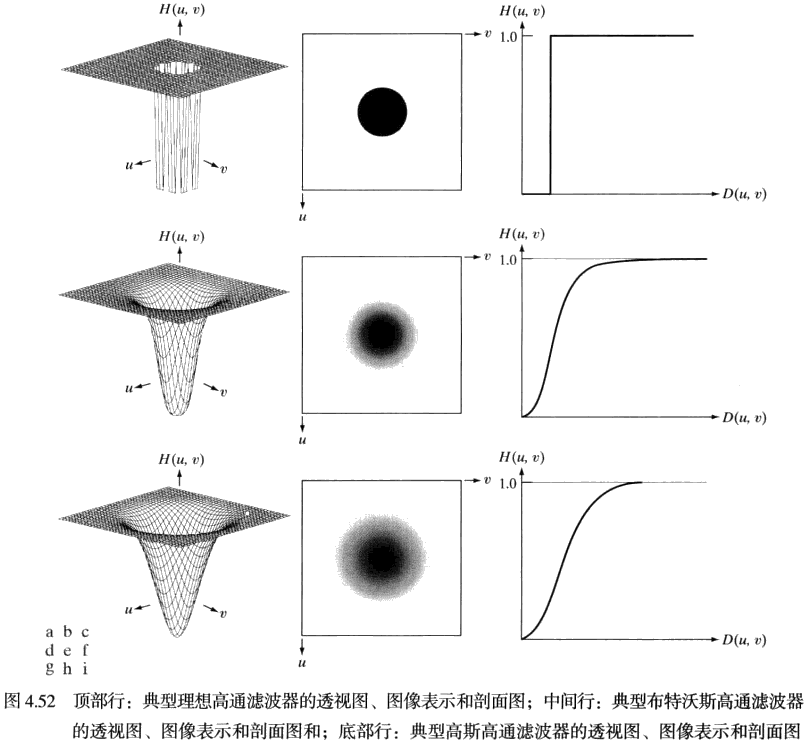
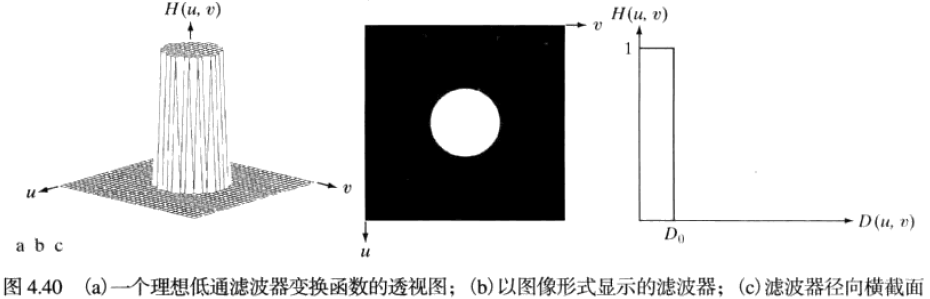
在以原点为圆心、以$D_0$ 为半径的圆内，无衰减地通过所有频率，而在圆外阻断所有频率的二维低通滤波器。在$H(μ,v)=1$和$H(μ,v)=0$之间的过渡点称为截止频率。

$$H(\mu, v)=\left\{\begin{array}{ll}1, & D(\mu, v) \leq D_{0} \\ 0, & D(\mu, v)>D_{0}\end{array}\right.$$

$$D(\mu, v)=[(\mu-\frac{P}{2})^2+(v-\frac{Q}{2})^2]^{1/2}$$

布特沃斯低通滤波器（BLPF）

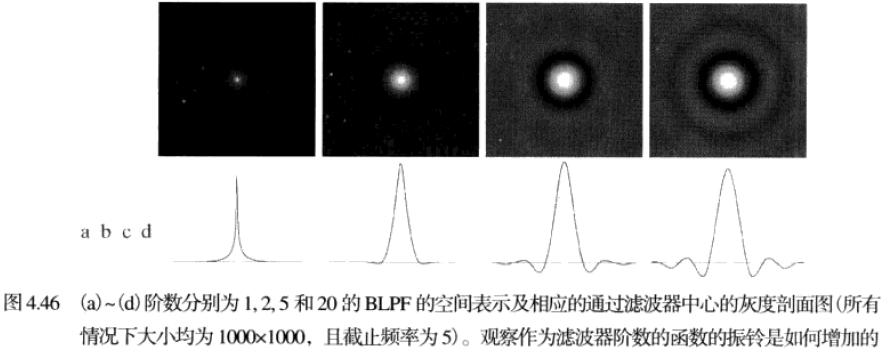
与 ILPF 不同，BLPF 没有在通过频率和滤除频率之间给出明显截止的急剧不连续性。空间域的一阶布特沃斯滤波器没有振铃现象，在二阶滤波器中振铃现象验很难察觉，更高阶的滤波器中振铃现象会很明显，其中阶数以$n$来代表。

$H(\mu, v)=\frac{1}{1+\left[D(\mu, v) / D_{0}\right]^{2 n}}$

高斯低通滤波器（GLPF）

GLPF 的傅里叶反变换也是高斯的，这意味着其 IDFT 得到的空间高斯滤波器将没有振铃。GLPF 以$σ$为关于中心的扩展度的度量，可通过令$σ=D_0$ 来使用上述 ILPF 和 BLPF 的表示法来表示 GLPF，$D_0$ 代表截止频率，当$D(μ,v)=D_0$ 时，GLPF 下降到其最大值的 0.607 处。

$$H(\mu, v)=e^{-D^{2}(\mu, v) / 2 \sigma^{2}}$$

$$H(\mu, v)=e^{-D^{2}(\mu, v) / 2 D_{0}{ }^{2}}$$

低通滤波的一种常用应用为“美容”处理，对于人脸，主要目的是减少皮肤细纹的锐化程度和小斑点。

4.4 高通滤波器

一个高通滤波器是从给定的一个低通滤波器得到的，设$H_{HP}(μ,v)$与$H_{LP}(μ,v)$分别表示高通和低通滤波器，则

这意味着被低通滤波器衰减的频率能通过高通滤波器，反之亦然。

$$H_{H P}(\mu, v)=1-H_{L P}(\mu, v)$$

理想高通滤波器（IHPF）

可以预料 IHPF 和 ILPF 具有相同的振铃性质：

$$H(\mu, v)=\left\{\begin{array}{ll}0, & D(\mu, v) \leq D_{0} \\ 1, & D(\mu, v)>D_{0}\end{array}\right.$$

布特沃斯高通滤波器（BHPF）

与低通版的一样，可以预料 BHPF 比 IHPF 更平滑，截止频率$D_0$ 越大，使用 BHPF 得到的结果就越平滑：

$$H(\mu, v)=\frac{1}{1+\left[D_{0} / D(\mu, v)\right]^{2 n}}$$

高斯高通滤波器（GHPF）

设截止频率距频率矩形中心距离为$D_0$ 。可以预料，GHPF 得到的结果比前两个滤波器的结果更平滑，即使是对微小物体和细线条得到的结果也是清晰的：

$$H(\mu, v)=1-e^{-D^{2}(\mu, v) / 2 D_{0}^{2}}$$

频率域的拉普拉斯算子

已知拉普拉斯算子对空间域图像可进行增强，其实它可得到频率域技术的等效结果：

• 拉普拉斯算子

  $$H(\mu, v)=-4\pi ^2(\mu^2+v^2)$$

• 拉普拉斯图像

  $$\nabla^{2} f(x, y)=\mathfrak{\Im}^{-1}\{H(\mu, v) F(\mu, v)\}$$

• 增强

  $$g(x, y)=\mathfrak{\Im}^{-1}\{F(\mu, v)-H(\mu, v) F(\mu, v)\}=\mathfrak{\Im}^{-1}\left\{\left[1+4 \pi^{2} D^{2}(\mu, v)\right] F(\mu, v)\right\}$$

其他

钝化模板、高提升滤波、高频强调滤波：参考 P.180。

同态滤波：参考 P.182。

4.5 指定频段/频率的滤波器

之前介绍的高通和低通滤波器在整个频率矩形上操作，在很多应用中，往往需要处理指定频段或频率矩形的小区域。指定频段的滤波器分别称为带阻滤波器或带通滤波器，指定频率的滤波器称为陷波滤波器。

带阻滤波器

设$D(μ,v)$是距频率矩形中点的距离，$D_0$ 是带宽的径向中心，$W$是带宽，以$H(μ,v)$代表滤波器，有

• 理想带阻滤波器

  $$H(\mu, v)=\left\{\begin{array}{lc} 0, & D_{0}-\frac{W}{2} \leq D \leq D_{0}+\frac{W}{2} \\ 1, & \text { the oters } \end{array}\right.$$

• 布特沃斯带阻滤波器

  $$H(\mu, v)=\frac{1}{1+\left[\frac{D W}{D^{2}-D_{0}^{2}}\right]^{2 n}}$$

• 高斯带阻滤波器

  $$H(\mu, v)=1-e^{-\left[\frac{D^{2}-D_{0}^{2}}{D W}\right]^{2}}$$

带通滤波器

设$H_{BR}(μ,v)$代表带阻滤波器，$H_{BP}(μ,v)$代表带通滤波器，其两者的关系与低通和高通滤波器之间的关系差不多：

$$H_{B P}(\mu, v)=1-H_{B R}(\mu, v)$$

陷波滤波器

更有用的选择性滤波器，其拒绝（或通过）事先定义的关于频率矩形中心的一个邻域的频率，进而选择性地修改 DFT 的局部区域。零相移滤波器必须是关于原点对称的，因此一个中心位于$(μ_0,v_0 )$的陷波在位置$(−μ_0,−v_0 )$必须有一个对应的陷波。

• 陷波带阻滤波器：通过中心已被平移到陷波滤波器中心的高通滤波器的乘积来构造。设$H_k(μ,v)$和$H_{−k}(μ,v)$是高通滤波器，它们的中心分别是$(μ_k,v_k )$和，$(-μ_k,-v_k )$中心根据频率矩形的中心$(M/2,N/2)$来确定，每个滤波器的距离$D_k (μ,v)$和$D_{−k}(μ,v)$由下式计算：

  $$H_{N R}(\mu, v)=\prod_{k=1}^{Q} H_{k}(\mu, v) H_{-k}(\mu, v)$$

  $$D_{k}(\mu, v)=\left[\left(\mu-\frac{M}{2}-\mu_{k}\right)^{2}+\left(v-\frac{N}{2}-v_{k}\right)^{2}\right]^{1 / 2}$$

  $$D_{-k}(\mu, v)=\left[\left(\mu-\frac{M}{2}+\mu_{k}\right)^{2}+\left(v-\frac{N}{2}+v_{k}\right)^{2}\right]^{1 / 2}$$

• 陷波带通滤波器：由陷波带阻滤波器得到

  $$H_{N P}(\mu, v)=1-H_{N R}(\mu, v)$$

5. 傅里叶变换的实现(FFT)

频率域计算工作的核心是傅里叶变换的运算，而傅里叶变换的正常运算复杂度为$O\left((MN)^2)\right.$，对于中等大小的图像（如$1024\times1024$像素），这意味着仅进行一次 DFT 就需要万亿次量级的乘法和加法，还不包括指数运算，即使是对超级计算机来说这也是一咱挑战。

故而有了快速傅里叶变换 FFT，使得复杂度降为$O(MN\log_2{MN})$，FFT 对计算量的减少另人印象深刻，如$1024\times 1024$像素的图像进行 FFT 只需要约 2000 万次乘法和加法运算，与前面的亿万次相比，降低非常明显。

具体方法就不介绍了，参照 P.188 或其他文献。