基础概念
1. 概述
一幅图像可定义为一个二维函数$f(x,y)$，在任何一对空间坐标$(x,y)$处的幅值$f$称为图像在该点处的强度或灰度。当$x,y$和灰度值$f$是有限的离散数值时，称该图像为数字图像。故数字图像由有限数量的元素组成，每个元素都有一个特定的位置和幅值，这些元素称为像素。
最主要的图像能源是电磁能谱（当然，还有其他成像方式，如声波成像在地质勘探、工业和医学中得到了应用）：
- 伽马射线成像：主要用途为核医学和天文观测
- X 射线成像：如医学（如 CT 成像）、天文学、工业
- 紫外线成像：平板印刷术、工业检测、显微方法、激光、生物成像、天文观测等
- 可见光及红外：光显微、天文、遥感、工业
- 微波：雷达
- 无线电波：医学和天文学
关于数字图像处理——
- 低级处理以输入、输出都是图像就特征
- 中级处理以输入为图像但输出是从这些图像中提取的特征（如边缘、轮廓及各物体的标识等）为特征
- 高级处理涉及“理解”已识别目标的总体，以及在连续统一体的远端执行与视觉相关的认知功能
数字图像处理的基本操作：
图像增强——对一幅图像进行某种操作，使其结果在特定应用中比原始图像更适合进行处理。注意，不存在增强图像的通用理论。
图像复原——图像增强是主观的，图像复原是客观的
小波——小波是以不同分辨率为描述图像的基础
压缩——减少图像存储量或降低传输图像带宽的处理
形态学处理——涉及提取图像成分，这些成分在表示和描述形状方面很有用
分割——将一幅图像划分为其组成部分或目标。通常，自动分割是数字图像处理中最困难的任务之一
识别——基于目标的描述给该目标赋予标志（譬如车辆）的过程
2. 人眼视觉系统
人眼视觉系统一些特性：
视觉系统往往会在不同强度区域的边界处出现“下冲”或“上冲”现像
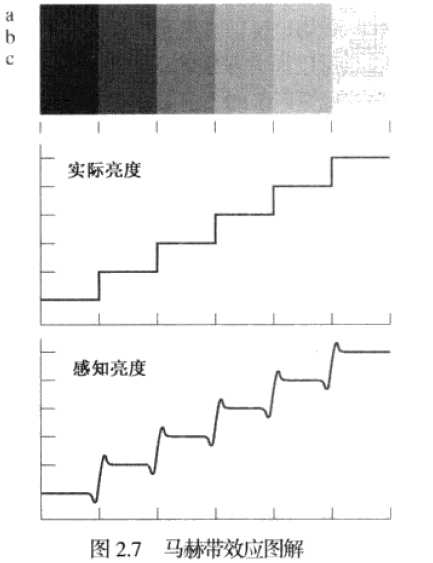
虽然条带的亮度恒定，但在靠近边界处我们实际上感知到了带有毛边的亮度模式。这些看起来带有毛边的带称为马赫带。
同时对比现象，即人眼的感知亮度并不简单地取决于图像的强度：
左图所有的中心方块都有完全相同的强度，但随着背景变得更亮（由左至右），它们在眼睛里会变得更暗。一个更熟悉的例子是一张白纸放在桌子上时看上去似乎比较白，而当使用它遮住眼睛来直视明亮的天空时，它看起来会总是呈现黑色
视错觉现象，即眼睛填充了不存在的信息或错误地感知了物体的几何特点
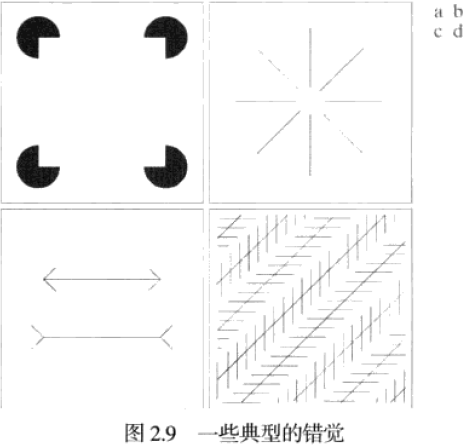
- a 中并没有定义一个正方形，却看起来如此明显
- b 中并没有定义一个圆，却看起来有一个圆
- c 中两条线段的长度是相等的，看起来却非如此
- d 中所有 45⁰ 方向的直线都是等间距的平行线
看到一个物体的电磁波的波长必须小于等于物体的尺寸。
3. 强度、灰度级、对比度
没有颜色的光称为单色光（或无色光），单色光的唯一属性是其强度（或大小）。由于在感知中单色光的强度从黑色到灰色变化，最后到白色，故通常用“灰度级”一词来形容单色光的强度，相应地，单色图像常称为灰度图像。
灰度级可表示为一个区间$[L_{min}, L_{max}]$，实际情况中常令该区间为$[0, L-1]$，其中$l=0$表示黑色，$l=L-1$表示白色，所有中间值为黑色到白色之间变化的灰度色调。出于存储和量化硬件考虑，灰度级数通常为 2 的整数次幂，即$L=2^k$，且各灰度级是等间隔的、区间$[0, L-1]$内的整数。当一幅图像有$2^k$个灰度级时，称该图像为一幅k 比特图像，最常用的为 8 比特图像。
一幅图像中最高和最低灰度级间的灰度差定义为对比度。当一幅图像中像素可感知的数值具有高动态范围时，认为该图像有高对比度；相对，具有低动态范围的图像很沉闷，看上去灰度被冲淡。
4. 数字图像表示
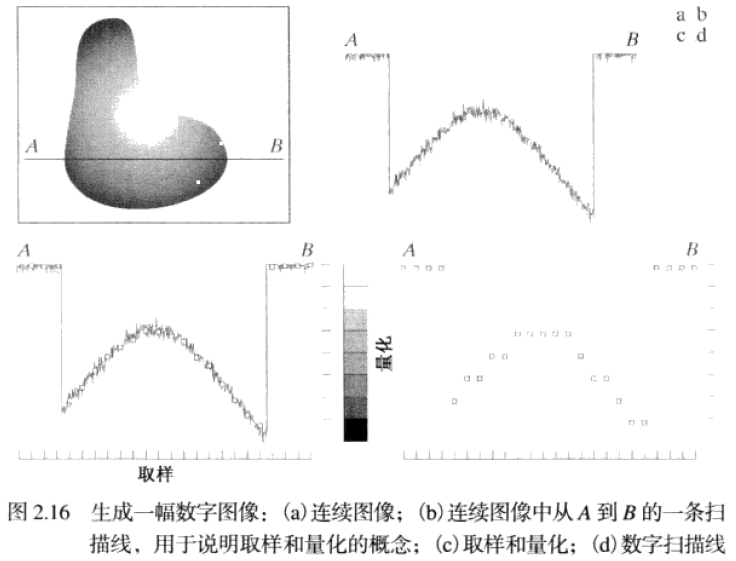
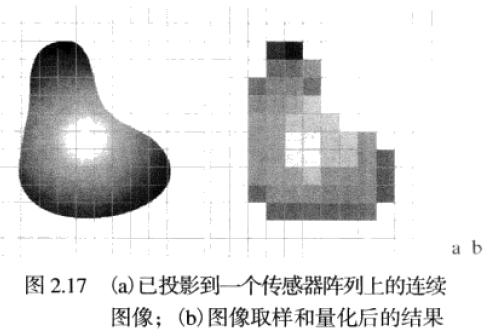
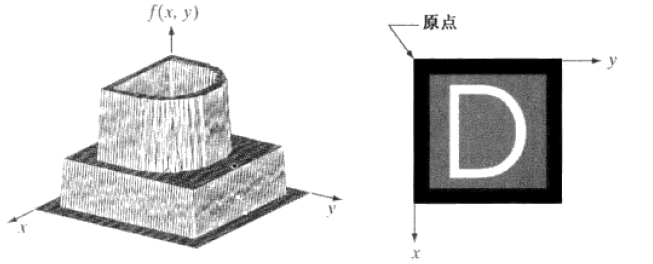
一幅图像有$x$和$y$坐标及幅度可能都是连续的，为将它转换为数字形式，须进行取样和量化操作。其中，对坐标值进行数字化称为取样，对幅值进行数字化称为量化。实践中，取样方法由用于生成该图像的传感器配置决定。很明显，数字图像的质量在很大程度上取决于取样和量化中所用的样本数和灰度级。
 |  |
|---|
若把一连续图像取样为一个二维阵列$f(x,y)$，该阵列包含有$M$行和$N$列，其中$(x,y)$是离散坐标，使用整数值$x=0,1,2,…,M−1$和$y=0,1,2,…,N−1$表示，图像在坐标$(x,y)$处的值记为$f(x,y)$。由一幅图像的坐标张成的实平面部分称为空间域，$x$和$y$称为空间变量或空间坐标，每个坐标$(x,y)$处的图像单元即是像素。当然，有时使用矩阵表示法表示数字图像及其像素其实更为方便。
 |  |
|---|---|
 |  |
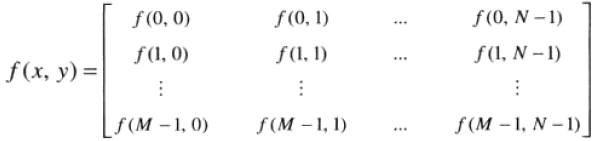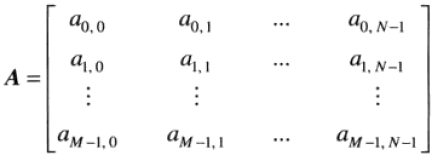空间分辨率与灰度分辨率？？？？？
图像内插是在诸如放大、收缩、旋转和几何校正等任务中广泛应用的基本工具。本质上，内插是用已知数据为估计未知位置的数值的处理。常用的内插方法如最近邻内插、双线性内插、双三次内插，其中双三次内插是商用图像编辑程序如 Adobe Photoshop 和 Corel Photopaint 的标准内插方法。
5. 图像的一些空间概念
坐标为$(x,y)$的像素$p$的相邻像素：
- 4 邻域：$N_4 (p)$，4 个水平和垂直的相邻像素
- 4 对角相邻：$N_D (p)$，4 个对角相邻像素
- 8 邻域：$N_8 (p)$，$N_4 (p)+N_D (p)$的 8 个像素
像素的相邻仅说明了两个像素在位置上的关系，若再加上取值相同或相近，则称两个像素邻接。关于取值相近，“$p,q∈V，其中V={v_1,v_2,…}$”称为灰度值相近（似）准则：
- 4 邻接：若$q∈N_4 (p)$，且$p,q∈V$，则$p$和$q$是 4 邻接的
- 8 邻接：若$q∈N_8 (p)$，且$p,q∈V$，则$p$和$q$是 8 邻接的
- m 领接/混合邻接：若$q∈N_4 (p)$或$q∈N_D (p)，p,q∈V$，且$N_4 (p)∩N_4 (q)$中没有来自$V$中数值的像素，则$p$和$q$是$m$邻接的。
4 邻接一定 8 邻接，反之不然；混合邻接的引入是为了消除8 邻接的二义性：
 |  |
|---|
令 S 是某图像的一个像素子集，设像素$p,q∈S$，若从$p$到$q$存在一个全部点都在$S$中的通路，则称$p$和$q$在$S$中是连通的。对于$S$中的任何像素$p$，$S$中连通到该像素的像素集称为$S$的连通分量；若$S$仅有一个连通分量，则集合$S$称为连通集/区域。连通性具有如下性质：
- $p$和$p$连通
- 若$p$与$q$连通，则$q$与$p$也连通
- 若$p$与$q$连通，$q$与$r$连通，则$p$与$r$连通
6. 图像处理的空间操作
阵列操作不同于矩阵运算，其是逐个元素进行的（其实就是 numpy 中 ndarray 的加减乘除那样的向量化运算）。在图像中进行的通常都是逐个像素执行的阵列操作，在图像中的算术操作作用如：
针对降噪的带噪图像相加（平均）
增强差别的图像相减
使用图像相乘和相除来校正阴影
单像素操作
令$z$代表原图像中像素的灰度，$s$是处理后图像中相应像素的灰度，有$s=T(z)$
邻域操作
令$S_{xy}$ 代表图像$f$中以任意一点$(x,y)$为中心的一个领域的坐标集，邻域处理在输出图像$g$中的相同坐标处生成一个相应的像素，该像素的值由输入图像中坐标在$S_{xy}$内的像素经指定操作决定。
几何空间变换
改进图像中像素间的空间关系，这种变换通常称为像皮膜变换。包含两个基本操作：
坐标的空间变换：$(x,y)=T{(v,w)}$，最常用的空间坐标变换$T$之一是仿射变换，其一般形式如下，这些变换可根据矩阵$\bold T$中元素所丢的值对一组坐标点做尺度、旋转(旋转是在保持直线特性方面最苛求的几何变换之一)、平移或偏移等
$\left[\begin{array}{lll}x & y & 1\end{array}\right]=\left[\begin{array}{lll}v & w & 1\end{array}\right] \boldsymbol{T}=\left[\begin{array}{lll}v & w & 1\end{array}\right]\left[\begin{array}{lll}t_{11} & t_{12} & 0 \ t_{21} & t_{22} & 0 \ t_{31} & t_{32} & 1\end{array}\right]$ 
灰度内插
7. 图像处理的概率方法
令$z_i,i=0,1,2,…,L−1$表示一幅$M×N$大小的数字图像中所有可能的灰度值，$n_k$ 为灰度$z_k$ 在图像中出现的次数，$MN$为像素总数，有：
灰度级$z_k$出现的概率$p(z_k)$：
$$ p(z_k )=n_k\over MN $$
平均灰度
$$ m=\sum_{k=0}^{L-1} Z_{k} p\left(z_{k}\right) $$
灰度的方差 （图像对比度的有用度量）
$$ \sigma{2}=\sum_{k=0}\left(z_{k}-m\right)^{2} p\left(z_{k}\right) $$
第$n$阶矩 $$ \mu_{n}(z)=\sum_{k=0}{L-1}\left(z_{k}-m\right) p\left(z_{k}\right) $$
8. 图像描绘子
这一部分本来应该挺重要，但是这本书实在太烂了，先忽略吧。需要时再查阅其它资料。
边界
选择用来作为描绘子的特征都应尽可能地对大小、平移和旋转不敏感。
边界描绘子：
| 形状数 | 傅里叶描绘子 | 统计矩 | |
|---|---|---|---|
| 长度 | |||
| 直径 | |||
| 偏心率 | |||
| 曲率 |
区域
区域描绘子：
| 拓扑描绘子 | 纹理 | 不变矩 | |
|---|---|---|---|
| 面积 | |||
| 周长 | |||
| 致密性 | |||
| 圆度率 |