数字

荒流2019年6月4日大约 4 分钟约 1237 字

格式化

使用format()函数格式化输出单个数字

	说明
`>>> x = 1234.56789`
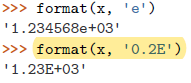	指数记数法
	同时指定宽度和精度的一般形式是`[<>^]?width[,]?(.digits)?`，其中 `width` 和 `digits` 为整数，`?`代表可选部分

舍入

对于简单的舍入运算，使用内置的round(value, ndigits)函数即可：

当一个值刚好在两个边界的中间的时候，round 函数返回离它最近的偶数，也就是对 1.5 或者 2.5 的舍入运算都会得到 2。
当传给 round()函数的 ndigits 参数为负数时，舍入运算会作用在十位、百位、千位等上面
舍入不同于格式化输出
如果你的目的只是简单的输出一定宽度的数，不需要使用 round()函数；同样，不要试着去舍入浮点值来“修正”表面上看起来正确的问题（对于大多数使用到浮点的程序没有必要也不推荐这样做，如果实际工程如金融领域实在不能允许这样的小误差，那就得考虑使用 decimal 模块了）。

数字的判等

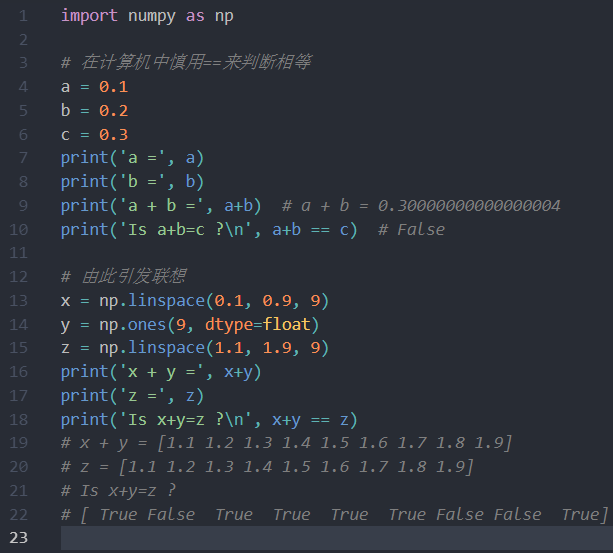
在编程中慎用==来对数字进行判断相等！

进制转换

将整数转换为二进制、八进制或十六进制的文本串，可以分别使用bin(), oct(), hex()函数：

示例	说明
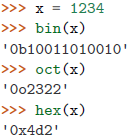	如果不想输出 0b, 0o 或者 0x 的前缀的话，可以使用 `format`()函数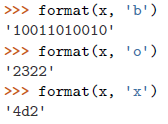
	为了以不同的进制转换整数字符串，使用带有进制的 `int()`函数即可
	注意 python 指定八进制的语法跟其他语言稍有不同，需确保八进制数的前缀是 0o。

字节与大整数

字节到大整数的打包与解包：

int.from_bytes()方法将 bytes 解析为整数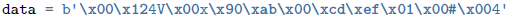
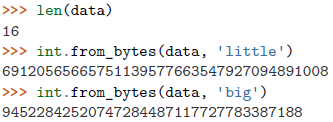
int.to_bytes()方法将一个大整数转换为一个字节字符串

无穷大与NaN

>>> a = float('inf')
>>> b = float('-inf')
>>> c = float('nan')

无穷大在执行数学计算的时候会传播
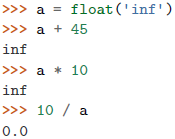
有些未定义的操作会返回一个 NaN
NaN 值会在所有操作中传播而不引起异常
NaN 值的一个特别之处是它们之间的比较操作总是返回 False
由于上条原因，测试一个 NaN 值的唯一安全方法就是使用 math.isnan()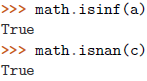

复数

复数可以使用函数 complex(real, imag) 或带有后缀 j 的浮点数来指定。其对应的实部、虚部、共轭复数可通过调用相应方法直接获取：

>>> a = complex(2, 4)
>>> b = 3 - 5j
>>> a
(2+4j)
>>> b
(3-5j)
>>> a.real
2.0
>>> a.imag
4.0
>>> a.conjugate()
(2-4j)

decimal模块

浮点数的一个普遍问题是它们并不能精确地表示十进制数，如果你想更加精确且能容忍一定的性能损耗，可以使用decimal（十进制的）模块。总的来说，decimal 模块主要用在金融领域。

尽管如此，依然得注意减法删除以及大数和小数的加法运算所带来的影响，如
```
>>> nums = [1.23e+18, 1, -1.23e+18]
>>> sum(nums) # Notice how 1 disappers
0.0
```
上面的错误可以利用 math.fsum() 所提供的更精确计算能力来解决：
```
>>> import math
>>> math.fsum(nums)
1.0
```

fractions模块

fractions模块可以被用来执行包含分数的数学运算，如：

>>> from fractions ipmort Fraction
>>> a = Fraction(5, 4)
>>> b = Fraction(7, 16)
>>> print(a + b)
27/16
>>> print(a * b)
35/64
>>> # Getting numerator/denominator
>>> c = a * b
>>> c.numerator
35
>>> c.denominator
64

random 模块

要从一个序列随机抽取一个元素，可以使用 random.choice()
随机提取出 N 个不同元素，可以使用 random.sample()
若仅仅想打乱序列中元素的顺序，可以使用 random.shuffle()
生成随机整数用 random.randint()，生成 0 到 1 范围内均匀分布的浮点数用 random.random()，获取 N 位随机位（二进制）整数用 random.getrandbits()
random 模块使用 Mersenne Twister（旋转梅森法）算法来生成随机数，这是一个确定性算法，但是可以通过 random.seet()函数修改初始化种子